Question

A wooden toy is made by scooping out a hemisphere of same radius from each end of a solid cylinder. If the height of the cylinder is 10cm, and its base is of radius 3.5cm, find the volume of wood in the toy. $\left( {\pi = \dfrac{{22}}{7}} \right)$

Answer 1

Hint: In this question remember that volume of toy can be found by Volume of cylinder – Volume of two hemispheres also remember to use formula of cylinder = $\pi {r^2}h$and volume of hemisphere = $\dfrac{2}{3}\pi {r^3}$, use this information to approach the solution.

Complete step-by-step answer:

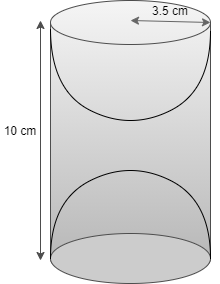
According to the given information from a solid cylinder of radius 3.5 cm and 10 cm a shape of hemisphere with the same radius of cylinder
So, the dimensions we have are
Height of the cylinder = 10 cm
Radius of base of cylinder = 3.5 cm
We know that formula for volume of cylinder is given as; ${v_1} = \pi {r^2}h$ (equation 1)
Substituting the values in equation (1) we get
${v_1} = \dfrac{{22}}{7}{\left( {3.5} \right)^2} \times 10$
${v_1} = 385c{m^3}$
The radius of hemispherical cavity that we are taking out is same as that of base of cylinder that is r = 3.5 cm
We know that formula for volume of hemisphere is given as; ${v_2} = \dfrac{2}{3}\pi {r^3}$ (equation 2)
Substituting the values in equation (2) we get
${v_2} = \dfrac{2}{3} \times \dfrac{{22}}{7} \times {(3.5)^3}$
${v_2} = 89.83c{m^3}$
Now a wooden toy is made by scooping out a hemisphere of same radius from each end of a solid cylinder, there are two ends in a cylinder so two hemispheres are taken out from the cylinder to form a toy.
$Volume{\text{ }}of{\text{ }}toy = Volume{\text{ }}of{\text{ }}cylinder - 2 \times Volume{\text{ }}of{\text{ }}hemisphere$
So, substituting the values in the above equation we get
$Volume{\text{ }}of{\text{ }}toy = 385 - \left( {2 \times 89.83} \right)$
$ \Rightarrow $$Volume{\text{ }}of{\text{ }}toy = 205.34c{m^3}$
Therefore, the Volume of toy is equal to $205.34c{m^3}$

Note: The key concept while solving such problems is simply to have a grasp of the formulas of various conic sections. When a conic cavity is taken out from another conic section then it eventually results in reduced volume of the remaining conic and this is what is being used above.