Question

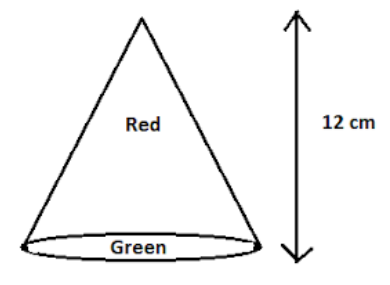
A wooden toy rocket is in the shape of a cone, as shown in figure. The height of the conical part is 12 cm. The base of the conical portion has a diameter of 10 cm. If the conical portion is to be painted red and the base portion green, find the area of the rocket to be painted. $\left( Use\,\pi =3.14 \right)$ .

(a) 282.85 sq.cm
(b) 200.25 sq.cm
(c) 252.75 sq.cm
(d) None of these

Answer 1

Hint: To start with, in the given problem we are dealing with a cone where we are to find the total area of the cone. The total area of the cone consists of the area of the curved surface area and the area of the base. So, we will find the areas of them differently and then add them to get our desired result.

Complete step by step solution:
According to the question, we are given a wooden cone where the height and diameter of the cone is given to us.
Now, we are to paint the total area of the cone. So, we will calculate the total area of the cone.
Area of rocket to be painted = Area of base + Curved surface area
As, the base is a circle, so, the area of the circle = $\pi \times {{\left( radius \right)}^{2}}$ sq. cm
Again, radius = $\dfrac{diameter}{2}=\dfrac{10}{2}cm=5\,cm$
Thus, area of base = $\pi \times {{\left( 5 \right)}^{2}}$ sq. cm $=25\pi $ sq. cm
And, now, area of curved surface = $\pi rl$ sq. cm where ${{l}^{2}}={{r}^{2}}+{{h}^{2}}$
Again, we know, r = 5 cm and h = 12 cm,
So, ${{l}^{2}}={{\left( 5 \right)}^{2}}+{{\left( 12 \right)}^{2}}=25+144=169$
Then, $l=\sqrt{169}=13\,cm$
Thus, area of curved surface = $\pi \times 5\times 13$ sq. cm $=65\pi $ sq. cm
So, we have now, area of the rocket $=65\pi +25\pi $ sq. cm $=90\pi $sq. cm
Again, as $\pi =3.14$ , then, area of the rocket is, $90\pi =\left( 90\times 3.14 \right)$ sq. cm = 282.85 sq.cm

So, the correct answer is “Option a”.

Note: In the given problem, we are dealing with the area of a cone. A cone is a shape formed by using a set of line segments or the lines which connects a common point, called the apex or vertex, to all the points of a circular base(which does not contain the apex). The distance from the vertex of the cone to the base is the height of the cone. The circular base has a measured value of radius. And the length of the cone from apex to any point on the circumference of the base is the slant height.