Question

(a). Write using Biot-Savart law, the expression for magnetic field $ \vec B $ due to an element $ \overrightarrow {dl} $ carrying current $ I $ at a distance $ \vec r $ from it in a vector form. Hence, derive the expression for the magnetic field due to the current carrying loop of radius $ R $ at a point P distant $ x $ from its center along the axis of the loop.
(b). Explain how Biot-Savart law enables one to express the Ampere’s circuital law in the integral form viz, $ \vec B.\overrightarrow {dl} = {\mu _0}I $ ; $ I $ is the total current passing through the surface.

Answer 1

Hint :Let us first understand the law of Biot-Savart. So, the Biot-savart law states that it calculates the magnetic field $ \overrightarrow {dB} $ due to an infinitesimal length of current carrying conductor. The total vector field is formed by integrating over the total length of the current carrying conductor. Let us consider the figure below of current carrying wire with infinitesimal length then the magnetic field at point P is given by
 $ \overrightarrow {dB} = \dfrac{{{\mu _0}I}}{{4\pi }}\dfrac{{\overrightarrow {dl} \times \hat r}}{{{r^2}}} $ ; $ \overrightarrow {dl} $ is the length of the conducting wire on which we are calculating the magnetic field produced by it, $ \vec r $ is the distance between wire and point P as shown in figure below:

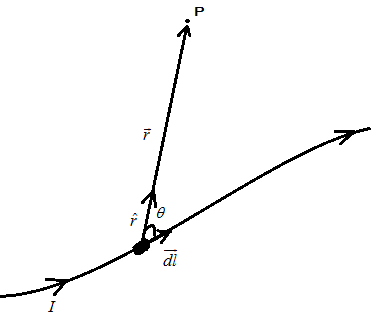
Complete Step By Step Answer:
(a) According to the Biot-Savart law explained above we have magnetic field due to current carrying conductor as:
 $ \overrightarrow {dB} = \dfrac{{{\mu _0}I}}{{4\pi }}\dfrac{{\overrightarrow {dl} \times \hat r}}{{{r^2}}} $ or $ \overrightarrow {dB} = \dfrac{{{\mu _0}I}}{{4\pi {r^3}}}\left( {\overrightarrow {dl} \times \vec r} \right) $
But here we have been asked about the magnetic field produced due to the current carrying loop as shown in the figure below:

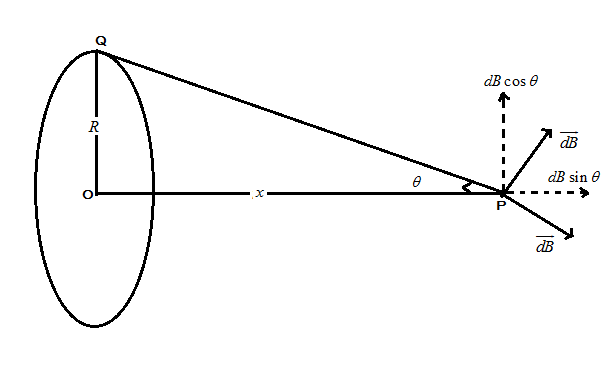
Here, according to the figure the vertical component of the magnetic field is cancelled out so the horizontal magnetic field element of $ \overrightarrow {dl} $ is given by:
According to the given data we have drawn the above figure such that $ R $ is the radii of the circular loop, point P is at distance $ x $ from the center of the loop and $ r $ is the distance between point P and the Q in the above figure.
Therefore, for horizontal component of the magnetic field from the above figure we have:
 $ dB = \dfrac{{{\mu _0}I}}{{4\pi {r^2}}}\sin \theta dl $
 $ \Rightarrow dB = \dfrac{{{\mu _0}IR}}{{4\pi {r^3}}}dl $ … (By using trigonometric ratios)
Now, on integrating both the sides we get:
 $ \Rightarrow \int {dB = \dfrac{{{\mu _0}IR}}{{4\pi {r^3}}}\int {dl} } $
But here by Pythagoras theorem we have
 $ r = {\left( {{R^2} + {x^2}} \right)^{\dfrac{1}{2}}} $
Therefore, the above equation is written as:
 $ \Rightarrow B = \dfrac{{{\mu _0}IR}}{{4\pi {{\left( {{R^2} + {x^2}} \right)}^{\dfrac{3}{2}}}}}2\pi R $ … (Since, $ \int {dl} = 2\pi R $ area of the circular loop)
 $ \therefore B = \dfrac{{{\mu _0}I{R^2}}}{{2{{\left( {{R^2} + {x^2}} \right)}^{\dfrac{3}{2}}}}} $
Thus, we have calculated the magnetic field produced by a circular loop at point P.
(b) Here, In the large current carrying conductor the magnetic field is given by Biot-Savart law as
 $ B = \dfrac{{{\mu _0}I}}{{2\pi R}} $
Above equation can also be written as
 $ \Rightarrow B \times 2\pi R = {\mu _0}I $
Or $ \int {\vec B.\overrightarrow {dl} = } {\mu _0}I $
Hence, we have determined the Ampere’s circuital law from the Biot-Savart law as shown above.

Note :
First of all we have to understand the concept and statement of the Biot-Savart law as we discussed in the above Hint part and understand the application of Biot-Savart law to carry out Ampere’s circuital law. Study the above question thoroughly and you will be able to answer any of this kind and you will also understand the whole concept of the Biot-Savart law.