Question

A yo-yo is resting on a perfectly rough horizontal table. Now, forces $F_1$ , $F_2$ and $F_3$ are applied separately as shown in the figure below. Assume that the horizontal component of the force $F_2$ is less than the kinetic friction. Then the correct statement is:

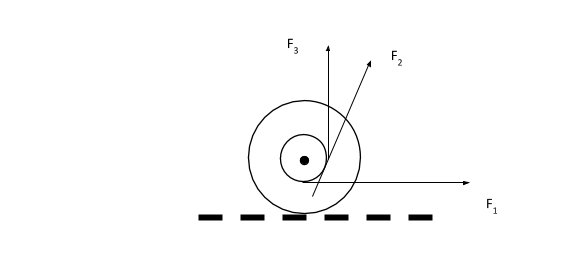
A) When $F_3$ is applied to the centre of mass moves to the right.
B) When $F_2$ is applied to the centre of mass moves to the left.
C) When $F_1$ is applied to the centre of mass moves to the right.
D) When $F_1$ is applied to the centre of mass moves to the right.

Answer 1

Hint:The centre of mass of the yo-yo paced on the horizontal surface when a force is applied to it. The direction of motion of the centre of mass will along the direction of the force applied. Here, out of the three forces applied to the yo-yo, only the force $F_1$ contributes to the movement of the yo-yo towards the right.

Complete step by step answer.
Step 1: Describe the effect on the centre of mass of the yo-yo when force $F_1$ is applied.
The force $F_1$ is directed towards the right. When the force $F_1$ is applied on the yo-yo, placed on the horizontal surface, the yo-yo moves along the direction of $F_1$ i.e., towards the right.
Therefore, on the application of the force $F_1$ the centre of mass of the yo-yo moves to the right.
 Step 2: Describe the effect on the centre of mass of the yo-yo when force $F_2$ is applied.
To explain the effect of the force $F_2$ on the yo-yo, we first resolve $F_2$ into its horizontal and vertical components, i.e. $F_2\cos \theta$ and $F_2\sin \theta$ .

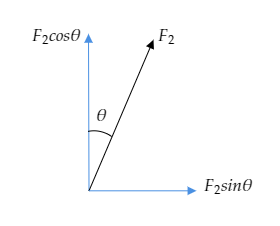
Here, only the horizontal component of $F_2$ contributes in the movement of the yo-yo towards the right or left. But it is given that the horizontal component $F_2\sin \theta$ is less than the kinetic friction. This means that the horizontal component $F_2\sin \theta$ will not cause the centre of mass to move towards the right or left.
Step 3: Describe the effect on the centre of mass of the yo-yo when force $F_3$ is applied.
The force $F_3$ acts vertically upwards. This can only cause the yo-yo to move upwards. Thus when $F_3$ is applied to the yo-yo, the centre of mass of the yo-yo cannot move towards the right.
Therefore, we can conclude that when force $F_1$ is applied, the centre of mass moves to the right.

Note: The surface on which the yo-yo resides is described as a perfectly rough horizontal surface. This implies that frictional forces are evident. When force $F_2$ was applied the yo-yo did not move. As mentioned before, this was because the horizontal component of $F_2$ was lesser than the kinetic friction i.e., the horizontal component of $F_2$ wasn’t strong enough to overcome the frictional force to produce an observable movement of the yo-yo.