Question

A(3,7); B(5,11), C(-2,8) are the vertices of $\Delta ABC$. AD is one of the medians of the triangle. The equation of the median AD is:
(a) $5x+3y-36=0$
(b) \[5x+3y+36=0\]
(c) $3y-5x-36=0$
(d) $3y-5x+36=0$

Answer 1

Hint: First look at the definition of median of triangle. Then find the midpoint of line BC. Here you have 2 points A, midpoint you are finding. Find the equation of line passing through these two points which is the required result. Line equation passing through\[\left( a,b \right);\text{ }\left( c,d \right)\text{ }is\text{ }\left( y-b \right)\text{ }=\dfrac{\left( d-b \right)}{\left( c-a \right)}\left( x-a \right)\].
Use this equation to get the required result.

Complete step-by-step solution -

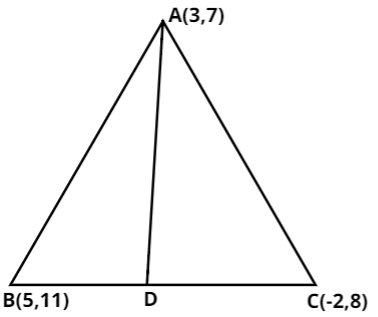
Median: The line passing through the vertex and midpoint of its opposite side is called a median.
Vertices given in the question A, B, C are written as:
$A\left( 3,7 \right);B\left( 5,11 \right);C\left( -2,8 \right)$
We want the equation of median through A already named as AD. By definition we get that D is mid-point of B, C points. So, we need to find that D. The midpoint of 2 points is the average of those two points. Let x-coordinate of D point be represented by x. Let y coordinated of D point be represented by y. we know x-coordinate B point is given as 5.
We know x coordinate of B point is given as 5
We know x coordinate of C point is given as -2
We know y coordinate of B point is given by as 11.
We know y coordinate of the C point is given as 8.
Be definition x coordinate of D is average of x coordinate of BC.
x= average of (5, -2)
By above equation, we can write x value as:
\[x=\dfrac{5-2}{2}\]
By simplifying, the above equation, we get x value as:
$x=\dfrac{3}{2}$
By definition y- coordinate of D is average of y of B, C:
y= Average (11, 8)
By above equation, we get it to be as:
$y=\dfrac{11+8}{2}$
By simplifying above equation, we get value of y as:
$y=\dfrac{19}{2}$
By x,y values we can point the D point as follows:
$D=\left( \dfrac{3}{2},\dfrac{19}{2} \right)$
So, we have two points \[A=\text{ }\left( 3,\text{ }7 \right)\] $D=\left( \dfrac{3}{2},\dfrac{19}{2} \right)$
So, line equation from (a, b) (c, d) is written as:
$\left( y-b \right)=\dfrac{\left( d-b \right)}{\left( c-a \right)}\left( x-a \right)$
Here we have a=3, b=7, c= $\dfrac{3}{2}$, d= $\dfrac{19}{2}$. By comparing
By substituting these values, we get the equation to be:
$y-7=\dfrac{\left( \dfrac{19}{2}-7 \right)}{\left( \dfrac{3}{2}-3 \right)}\left( x-3 \right)$
By cross multiplying and bring all terms to one side:
\[5\left( x-3 \right)+3\left( y-7 \right)=0\]
By simplifying the, brackets we get it as:
$5x-15+3y-21=0$
By adding the constants, we get $5x+3y-36=0$
Therefore option (a) is correct.

Note: Be careful while taking average, take care of the “-“sign in the coordinate of points. While removing the brackets at the last step don’t forget to multiply with constant in hurry students multiply only to variables and leave the constant as it is but it is totally wrong you must multiply to both.