Question

$\text{AAS}\left( \text{or SAA} \right)\text{ test:}$
The sum of the measures of angles in a triangle is ${{180}^{0}}$. Therefore, if two corresponding pairs of angles in two triangles are congruent, then the remaining pair of angles is also congruent. Hence if two angles and a side adjacent to one of them are congruent with corresponding parts of the other triangle then the condition for ASA test is fulfilled. So, the triangles are congruent.

Answer 1

Hint: Assume any two of the triangles and find the sum of the angles in a triangle and equal it to $180{}^\circ $. Take any two of the corresponding angles as equal/congruent in two triangles and find the value of the third angle in two triangles to show that the remaining pair of angles are also equal or congruent. Then assume one of the sides adjacent to one of the angles is congruent to the corresponding side in another triangle. Now compare the two triangles and use the Side Angle Angle rule to get the result. Side Angle Angle rule is used to check the congruency of two triangles and defined as If the two angles and one side of a triangle is congruent with the corresponding angles and sides of another triangle, then the two triangles are congruent.

Complete step by step answer:

Let us take the two triangles $\Delta ABC,\Delta DEF$ as shown in below figure

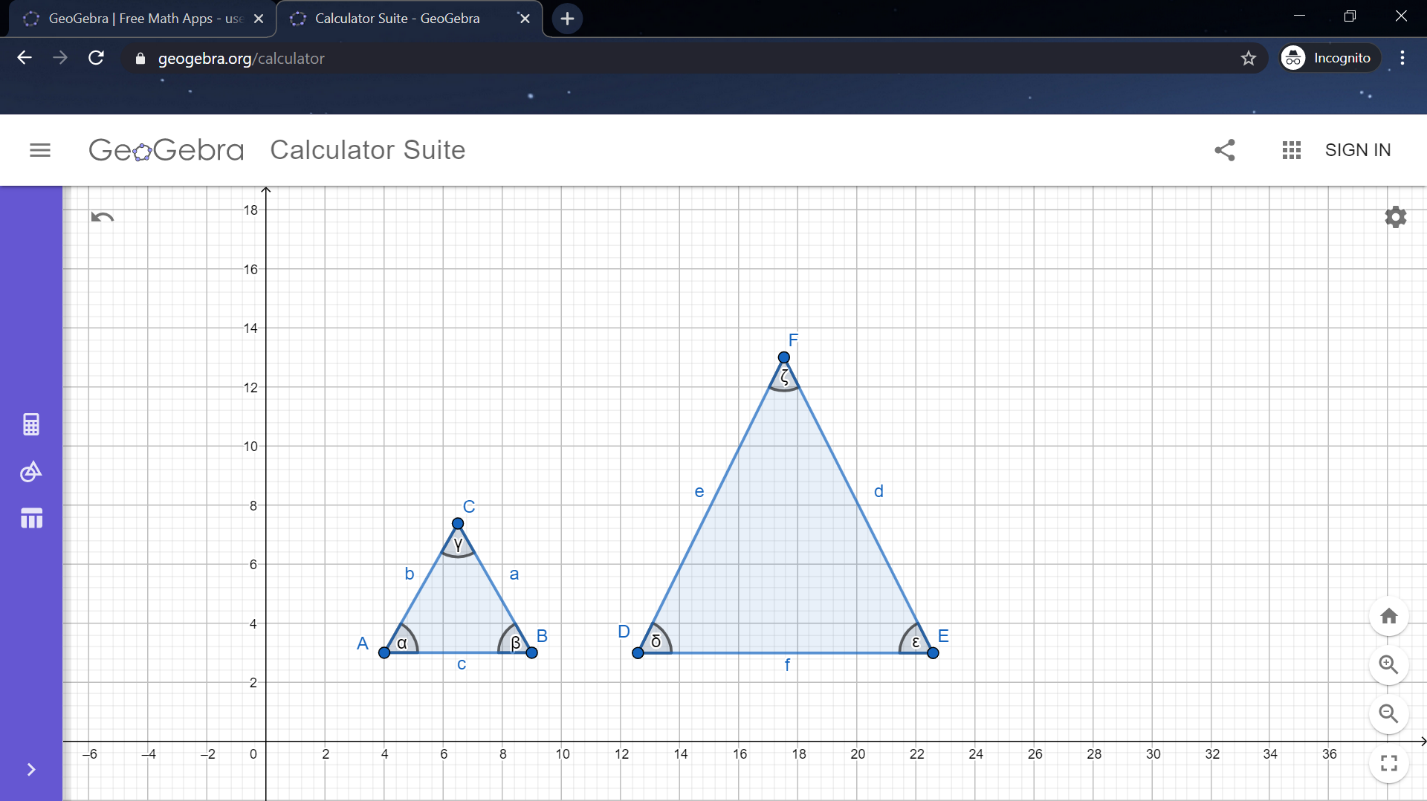
$\Rightarrow$ From the above triangles
$\Rightarrow$ Length of $BC=a$
$\Rightarrow$ Length of $AC=b$
$\Rightarrow$ Length of $AB=c$
$\Rightarrow$ Length of $EF=d$
$\Rightarrow$ Length of $DF=e$
$\Rightarrow$ Length of $DE=f$
$\Rightarrow$ The angle $\angle BAC=\alpha $
$\Rightarrow$ The angle $\angle ABC=\beta $
$\Rightarrow$ The angle $\angle ACB=\gamma $
$\Rightarrow$ The angle $\angle EDF=\delta $
$\Rightarrow$ The angle $\angle DEF=\varepsilon $
$\Rightarrow$ The angle $\angle DFE=\zeta $
Given that, the sum of all the measures of the angles in a triangle is $180{}^\circ $, then
$\alpha +\beta +\gamma =180{}^\circ $ and $\delta +\varepsilon +\zeta =180{}^\circ $
Now the sum of all the angles in the two triangles is
$\begin{align}
  & \alpha +\beta +\gamma +\delta +\varepsilon +\zeta =180{}^\circ +180{}^\circ \\
 & =360{}^\circ
\end{align}$
If $\alpha =\delta =x$ and $\beta =\varepsilon =y$ then the values of $\gamma ,\zeta $ are
$\gamma =180{}^\circ -\left( \alpha +\beta \right)$ and $\zeta =180{}^\circ -\left( \delta +\varepsilon \right)$
Substituting the values of $\alpha ,\beta ,\delta ,\varepsilon $ in the above equations then we have
$\gamma =180{}^\circ -\left( x+y \right)$ and
$\begin{align}
  & \zeta =180{}^\circ -\left( x+y \right) \\
 & =\gamma
\end{align}$
$\Rightarrow$ From the equation, we can say that ‘In two triangles the pair of corresponding angles are equal/congruent and the sum of all the angles in a triangle are equal/congruent to $180{}^\circ $ then the remaining angles of the two triangles are equal’.
If the length of $AB$ is equal/congruent to the length of $DE$. Now let us compare the two triangles
We have
$\alpha =\delta $
$\beta =\varepsilon $
Then automatically $\gamma =\zeta $
$\Rightarrow$ And $AB=pDE$
$\Rightarrow$ Where $p$ is the constant.
$\Rightarrow$ We know that in two triangles the two angles and one corresponding side is equal/congruent to the corresponding angles and side in another triangle then the two triangles are congruent to each other on the Side Angle Angle rule.

Note:
Please recognize the difference between equal and congruent. If the value of two angles is the same then we can say the two angles are equal. But if the value of one angle is in proportion with the value of another angle then we can say that the two angles are congruent. Mathematically $\alpha =p\beta $ . Here the angle $\alpha $ is in$p$ times proportion with $\beta $ . Now the angles $\alpha ,\beta $ are congruent. In this problem, we use the property equal instead of congruent to better simplification and understanding.