Question

AB is a line segment. C and D are points on opposite sides of AB such that each of them is equidistant from the point A and B as in the figure. The line CD is the perpendicular bisector of AB.
A. True
B. False

Answer 1

Hint: In order to prove that whether the above statement is true or false, we will proceed by using the concept of congruent triangles such that it will give us the required condition i.e. to prove the perpendicular bisector. Then by using the linear pair axiom we will be able to prove the condition true or false.

Complete step-by-step answer:
In this question, we are given that

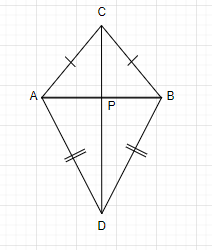
C and D are equidistant from points A and B.
Also CA = CB and DA = DB are given.
We have to prove that $CD \bot AB$, $\angle APC = \angle BPC = {90^ \circ }$
Now we will take two triangles $\vartriangle CAD{\text{ and }}\vartriangle CBD$
Where AC = BC (given)
Also AD = BD (given)
And DC = DC (common)
$\therefore \vartriangle CAD \cong \vartriangle CBD$ (by using Side Side Side congruence rule)
Hence $\angle ACD = \angle BCD$ (C.P.C.T)
Similarly in $\vartriangle CAPand\vartriangle CBP$
 AC = BC(given)
$\angle APC = {90^ \circ }$ (right angle triangle)
And CP = CP(common)
$\therefore \vartriangle CAP \cong \vartriangle CBP$(by using Side Angle Side congruence rule)
Hence AP = BP (corresponding parts of congruent triangles [C.P.C.T])
Also $\angle APC = \angle BPC$(corresponding parts of congruent triangles [C.P.C.T])
Since AB is a line segment and also we know that the measure of a straight angle is ${180^ \circ }$.
$\therefore \angle APC + \angle BPC = {180^ \circ }$(linear pair axiom)
 Also we can rewrite it as –
$ \Rightarrow 2\angle APC = {180^ \circ }$
$\therefore \angle APC = {90^ \circ }$
Or $\angle APC = \angle BPC = {90^ \circ }$
Hence AC = BC and $\angle APC = \angle BPC = {90^ \circ }$
$\therefore $ CD is the perpendicular bisector of AB.
$ \Rightarrow $ The above statement is proven right.
Option A is right.

Note: In this question, one can get confused while using the appropriate test of congruent triangles as we used two properties here which are SAS and SSS but there are also other tests to prove the congruence of the triangles which are ASA (Angle Side Angle) and (Angle Angle Side).