
ABC and DBC are two isosceles triangles on the same side of BC. Then DA (or AD ) produced bisects the BC at the right angle.
If the statement is true mention 1 otherwise 0.
Answer
498.6k+ views
Hint: Prove the congruence of the pair of triangles DBA and DCA and then DBE and DCE to conclude BE=CE where E is the point where DA intersects BC. Prove the congruence of triangles ABE and ACE to prove
Complete step-by-step solution:
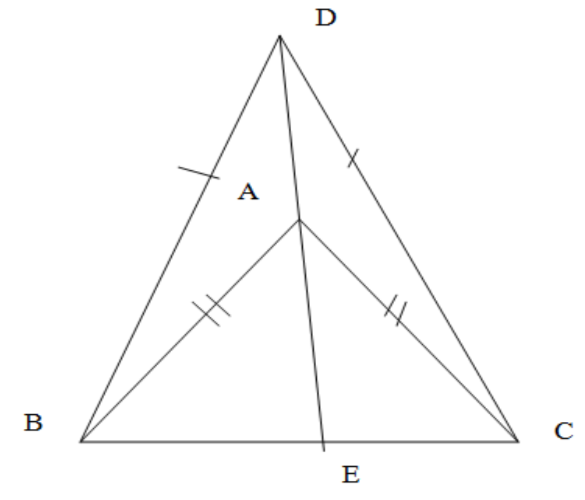
We have drawn the figure as required by the question where the triangles ABC and DBC are on the same side of BC. It is given in the question that the triangles ABC and DBC are isosceles where the equal sides in
We are asked to check whether
We observe the triangles DBA and DCA where we already have AB=AC and DB=DC. They also have common side AD. So by side-side-side congruence we get
We again observe the triangles DBE and DCE where we already have DB=DC ,
We observe the triangles ABE and CDE where we already have BE=CE(proved above), AB=AC and the common side AE. Using side-side-side congruence we have
We have
Note: The important thing to be careful of here is different types of congruence. If we pick any combination from sides and angles of one triangle and find them to be equal to sides or angles of another triangle they are not necessarily congruent, for example, angle-angle-angle equality where the triangles are similar but not congruent.
Complete step-by-step solution:

We have drawn the figure as required by the question where the triangles ABC and DBC are on the same side of BC. It is given in the question that the triangles ABC and DBC are isosceles where the equal sides in
We are asked to check whether
We observe the triangles DBA and DCA where we already have AB=AC and DB=DC. They also have common side AD. So by side-side-side congruence we get
We again observe the triangles DBE and DCE where we already have DB=DC ,
We observe the triangles ABE and CDE where we already have BE=CE(proved above), AB=AC and the common side AE. Using side-side-side congruence we have
We have
Note: The important thing to be careful of here is different types of congruence. If we pick any combination from sides and angles of one triangle and find them to be equal to sides or angles of another triangle they are not necessarily congruent, for example, angle-angle-angle equality where the triangles are similar but not congruent.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




