
ABC is a right – angled triangle with
Answer
493.2k+ views
Hint: We were given that ABC is a right-angled triangle with
Complete step-by-step solution
Let us represent the triangle from the given details of the question. From the question, we were given that ABC is a right-angled triangle with
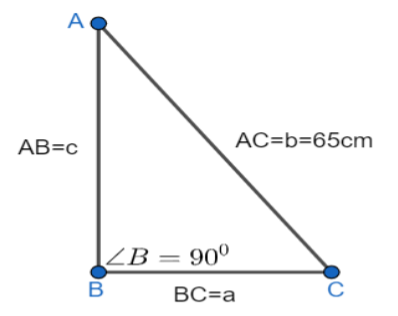
We know that if A, B, and C are angles of a triangle and a, b and c are the lengths of the sides of a triangle and R is the circumradius then
Now we will apply sine rule for the triangle ABC, then we get
From equation (1), we can write
We know that the angles of a triangle is equal to
So, we can write
We know that if r is inradius of a triangle, A, B and C are angles of a triangle and R is circumradius of a circle then
Now we will apply this formula for the triangle ABC, then we get
Now let us substitute equation (1), equation (2) and equation (3) in equation (4), then we get
We know that
So, now we will write
We know that
Now we will square equation (5) on both sides, then we get
We know that
We know that
We know that
We know that if A, B and C are angles of a triangle and
So, let us assume the area of the triangle is equal to
So, let us substitute equation (2), equation (3) in equation (7), then we get
Now let us substitute equation (6) in equation (8), then we get
We know that
So, it is clear that the value of
From the question, it is clear that abc is equal to 504.
Then from equation (10) and equation (11), we will get
So, the value of
Hence, option A is correct.
Note: Students should know that if A, B, and C are angles of a triangle and a, b and c are the lengths of the sides of a triangle and R is the circumradius then
Complete step-by-step solution
Let us represent the triangle from the given details of the question. From the question, we were given that ABC is a right-angled triangle with

We know that if A, B, and C are angles of a triangle and a, b and c are the lengths of the sides of a triangle and R is the circumradius then
Now we will apply sine rule for the triangle ABC, then we get
From equation (1), we can write
We know that the angles of a triangle is equal to
So, we can write
We know that if r is inradius of a triangle, A, B and C are angles of a triangle and R is circumradius of a circle then
Now we will apply this formula for the triangle ABC, then we get
Now let us substitute equation (1), equation (2) and equation (3) in equation (4), then we get
We know that
So, now we will write
We know that
Now we will square equation (5) on both sides, then we get
We know that
We know that
We know that
We know that if A, B and C are angles of a triangle and
So, let us assume the area of the triangle is equal to
So, let us substitute equation (2), equation (3) in equation (7), then we get
Now let us substitute equation (6) in equation (8), then we get
We know that
So, it is clear that the value of
From the question, it is clear that abc is equal to 504.
Then from equation (10) and equation (11), we will get
So, the value of
Hence, option A is correct.
Note: Students should know that if A, B, and C are angles of a triangle and a, b and c are the lengths of the sides of a triangle and R is the circumradius then
Latest Vedantu courses for you
Grade 10 | CBSE | SCHOOL | English
Vedantu 10 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




