Question

ABC is a triangle. D is a point on AB such that $AD = \dfrac{1}{4}AB$and E is a point on AC such that $AE = \dfrac{1}{4}AC$. If DE = 2cm, find BC.
$
  A{\text{ 10cm}} \\
  {\text{B 8cm}} \\
  {\text{C 4cm}} \\
  {\text{D 6cm}} \\
 $

Answer 1

Hint- Here we will proceed by using the given conditions i.e. $AD = \dfrac{1}{4}AB$and $AE = \dfrac{1}{4}AC$to make the triangles similar. Then we will find the length of side BC when we will substitute the value of DE.

Complete step by step answer:

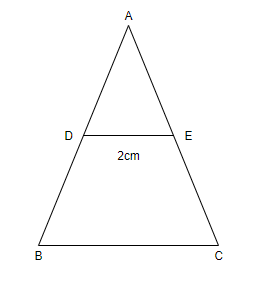
As we are given that-
ABC is a triangle.
D is a point on AB such that $AD = \dfrac{1}{4}AB$.
 E is a point on AC such that $AE = \dfrac{1}{4}AC$.
And if DE = 2cm
Now we have to find the BC.
$ \Rightarrow AD = \dfrac{1}{4}AB$
By cross- multiplication, we get-
$ \Rightarrow \dfrac{{AD}}{{AB}} = \dfrac{1}{4}$
In $\vartriangle ADE$ and $\vartriangle ABC$,
$AE = \dfrac{1}{4}AC$
$\angle A = \angle A$ (common)
$AD = \dfrac{1}{4}AB$
$\vartriangle ADE \sim \vartriangle ABC$(SAS rule)
As we can see that the length of two corresponding sides is in the same proportion and the included angle between the sides is common.
Then the triangles are similar using Side Angle Side rule.
$ \Rightarrow \dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}} = DEBC$
$ \Rightarrow \dfrac{1}{4} = \dfrac{2}{{BC}}$
Or BC = 8cm.
Therefore, the length of BC is 8cm,
Hence option B is right.
Note- In order to solve this type of question, we must know the properties of triangles. Along with that we must know all the rules i.e. SSS, ASA, SAS, AAS to solve similar kinds of problems.