Question

ABC is an isosceles triangle and $\mathrm{\angle }B={90}^{\circ }$, then show that $A{C}^2=2A{B}^2$.

Answer 1

Hint-In this particular type of question we have to proceed by using the property of isosceles triangle in the given triangle. Then we need to apply the Pythagoras theorem on the sides of the triangle since angle B is equal to 90 degrees to get the desired answer.

Complete step-by-step answer:

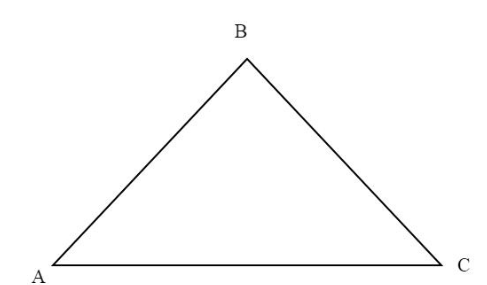
ABC is an isosceles triangle and
In $△ABC$, $\mathrm{\angle }B={90}^{\circ }$
AB = BC (Since $△ABC$ is an isosceles triangle and two sides of isosceles triangle are equal)
Now using Pythagoras theorem in right triangle ABC,
$A{C}^2=A{B}^2+B{C}^2$ (Sum of square of two side of a triangle is equal to square of third side)
$\begin{array}{c}\Rightarrow A{C}^2=A{B}^2+A{B}^2\left(\text{since AB = BC}\right)\\ \Rightarrow A{C}^2=2A{B}^2\end{array}$
Note-Remember to recall the basic properties of the isosceles triangle and Pythagoras theorem. Note that an isosceles triangle is a triangle with two sides equal to each other. Keeping the figure in mind is beneficial while solving this type of question.