
$ABC$ is an isosceles triangle in which $AB = AC$ .$AD$ bisects exterior angle $QAC$ and $CD\parallel AB$ . Show that
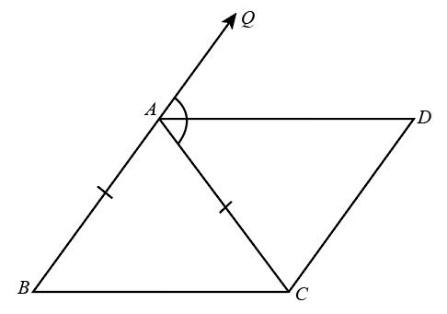
(i)$\angle DAC = \angle BCA$
(ii)$ABCD$ is a parallelogram

Answer
575.4k+ views
Hint: To prove the given conditions we will use the properties of the triangles. The angles which are opposite to the equal sides must always be equal to each other. Since $AB$ and $AC$ are equal, therefore the side opposite to these sides will be equal. Also $AD$ is the bisector of the exterior angle, we will use this condition to find the relation between the angles. We will use the exterior angle property which says that the sum of the two opposite sides interior angles must always be equal to the exterior angle. In the second part of the question we need to prove that the given quadrilateral is a parallelogram for that we will prove that the pair of opposite sides in the quadrilateral $ABCD$ are parallel to each other with the help of the result of the first part.
Complete step by step solution
Given:
The triangle $\Delta ABC$ is an isosceles triangle such that $AB = AC$ . Also, $AD$ bisects $\angle QAC$ and $CD\parallel AB$.
(i)
Since $AD$ bisects $\angle QAC$. Therefore, the angle $QAD$ and angle $DAC$ will be equal which can be expressed as:
$\angle QAD = \angle DAC = \dfrac{1}{2}\angle QAC$ ……(i)
Also, it is given in the question that $AB = AC$.
We know from the properties of the triangle that angles which are opposite to the equal sides must always be equal. Therefore, angle opposite to side $AB$ and $AC$ must be equal which can be expressed as:
$\angle BCA = \angle ABC$ ……(ii)
Now we will consider $\Delta ABC$, we have angle $QAC$ is the exterior angle.
Now from the properties of the triangles, we know that the sum of the interior angles which are opposite to each other must be equal to exterior angle which can be expressed as:
$\angle QAC = \angle ABC + \angle BCA$
We know from equation (ii) $\angle BCA = \angle ABC$.
$\begin{array}{l}
\angle QAC = \angle BCA + \angle BCA\\
\angle QAC = 2\angle BCA
\end{array}$
We can rewrite the above expression as:
$\dfrac{1}{2}\angle QAC = \angle BCA$
We know from equation (i) $\angle DAC = \dfrac{1}{2}\angle QAC$.
$\angle DAC = \angle BCA$
Hence, the given condition is proved.
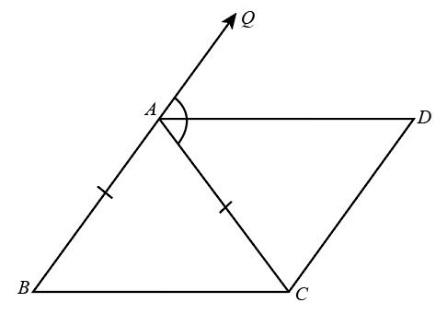
(ii)
)
As we have proved in the first part that $\angle DAC = \angle BCA$ .
So, we can say that for the lines $BC$ and $AD$,$AC$ is the transversal.
But we know that $\angle DAC$ and$\angle BCA$ are the alternate interior angles and from the given expression they are equal. So we can conclude that lines $BC$ and $AD$ are parallel to each other which can be expressed as $BC\parallel AD$ .
Now we will consider quadrilateral $ABCD$ . As it is given in the question $CD\parallel AB$ . Also, we have proved above that $BC\parallel AD$.
Since the pair of opposite sides are parallel to each other, hence we can say that quadrilateral $ABCD$ is a parallelogram.
Note: To solve this question, we should have prior knowledge about the properties of triangles and its different angles. Here we are using the exterior angle property and angle bisector theorem. Also, we should have prior knowledge about the properties of parallelogram.
Complete step by step solution
Given:
The triangle $\Delta ABC$ is an isosceles triangle such that $AB = AC$ . Also, $AD$ bisects $\angle QAC$ and $CD\parallel AB$.
(i)

Since $AD$ bisects $\angle QAC$. Therefore, the angle $QAD$ and angle $DAC$ will be equal which can be expressed as:
$\angle QAD = \angle DAC = \dfrac{1}{2}\angle QAC$ ……(i)
Also, it is given in the question that $AB = AC$.
We know from the properties of the triangle that angles which are opposite to the equal sides must always be equal. Therefore, angle opposite to side $AB$ and $AC$ must be equal which can be expressed as:
$\angle BCA = \angle ABC$ ……(ii)
Now we will consider $\Delta ABC$, we have angle $QAC$ is the exterior angle.
Now from the properties of the triangles, we know that the sum of the interior angles which are opposite to each other must be equal to exterior angle which can be expressed as:
$\angle QAC = \angle ABC + \angle BCA$
We know from equation (ii) $\angle BCA = \angle ABC$.
$\begin{array}{l}
\angle QAC = \angle BCA + \angle BCA\\
\angle QAC = 2\angle BCA
\end{array}$
We can rewrite the above expression as:
$\dfrac{1}{2}\angle QAC = \angle BCA$
We know from equation (i) $\angle DAC = \dfrac{1}{2}\angle QAC$.
$\angle DAC = \angle BCA$
Hence, the given condition is proved.
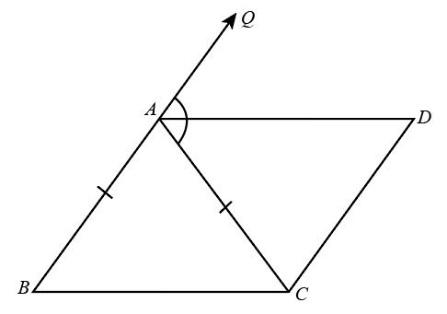
(ii)
)

As we have proved in the first part that $\angle DAC = \angle BCA$ .
So, we can say that for the lines $BC$ and $AD$,$AC$ is the transversal.
But we know that $\angle DAC$ and$\angle BCA$ are the alternate interior angles and from the given expression they are equal. So we can conclude that lines $BC$ and $AD$ are parallel to each other which can be expressed as $BC\parallel AD$ .
Now we will consider quadrilateral $ABCD$ . As it is given in the question $CD\parallel AB$ . Also, we have proved above that $BC\parallel AD$.
Since the pair of opposite sides are parallel to each other, hence we can say that quadrilateral $ABCD$ is a parallelogram.
Note: To solve this question, we should have prior knowledge about the properties of triangles and its different angles. Here we are using the exterior angle property and angle bisector theorem. Also, we should have prior knowledge about the properties of parallelogram.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
The shortest day of the year in India

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




