Question

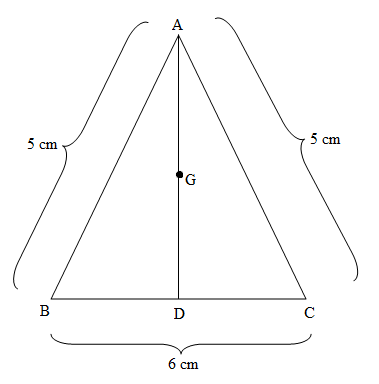
ABC is an isosceles triangle with AB = AC = 5 and BC = 6. If G is the centroid of $\Delta ABC$, then AG is equal to
\[
  A.{\text{ }}\dfrac{1}{3} \\
  B.{\text{ }}\dfrac{2}{3} \\
  C.{\text{ }}\dfrac{4}{3} \\
  D.{\text{ }}\dfrac{8}{3} \\
 \]

Answer 1

Hint: In order to solve this question first we will determine the median of the isosceles triangle and by the property of ratio of proportion we will proceed.

Complete step-by-step solution -
Since the given triangle is isosceles, so the median and altitude will coincide.
So, $\Delta ABD$ is a right angle triangle at D.
As we know by the Pythagoras theorem.
${\left( {{\text{Hypotenuse}}} \right)^2}{\text{ = }}{\left( {{\text{base}}} \right)^2}{\text{ + }}{\left( {{\text{height}}} \right)^2}$
By using Pythagoras theorem in above triangle ABD
$
   \Rightarrow {\left( {AB} \right)^2} = {\left( {AD} \right)^2} + {\left( {BD} \right)^2} \\
   \Rightarrow {\left( 5 \right)^2} = {\left( {AD} \right)^2} + {\left( 3 \right)^2}{\text{ }}\left[ {\because BD = \dfrac{1}{2}BC,{\text{ since AD is median}}} \right] \\
 $
Let us find the value of AD.
\[
   \Rightarrow {\left( {AD} \right)^2} = {\left( 5 \right)^2} - {\left( 3 \right)^2} \\
   \Rightarrow {\left( {AD} \right)^2} = 25 - 9 \\
   \Rightarrow {\left( {AD} \right)^2} = 16 \\
   \Rightarrow AD = \sqrt {16} \\
   \Rightarrow AD = 4cm \\
 \]
As we have now got the value of AD.
As we know that the centroid of the triangle divides the altitude into a 2:1 ratio.
So, $AG:GD = 2:1$
So, let us apply ratio and proportion for altitude.
$
  AG = \dfrac{2}{3} \times AD \\
  AG = \dfrac{2}{3} \times 4 \\
   \Rightarrow AG = \dfrac{8}{3} \\
 $
Hence, the value of AG is $\dfrac{8}{3}$.
So, option D is the correct option.

Note: The centroid or geometric center of a plane figure is the arithmetic mean position of all the points in the figure. Informally, it is the point at which a cutout of the shape could be perfectly balanced on the tip of a pin. The centroid of a triangle is the intersection of the three medians of the triangle (each median connecting a vertex with the midpoint of the opposite side).