Question

ABC is an isosceles triangle with AC = BC . If \[A{B^{2\;}} = {\text{ }}2{\text{ }}A{C^2}\]. Prove that ABC is a right angle triangle

Answer 1

Hint:Because angles opposite equal sides are themselves equal, an isosceles triangle has two equal angles (the ones opposite the two equal sides). Thus, given two equal sides and a single angle, the entire structure of the triangle can be determined.
The Pythagorean equation relates the sides of a right triangle in a simple way, so that if the lengths of any two sides are known the length of the third side can be found. Another corollary of the theorem is that in any right triangle, the hypotenuse is greater than any one of the other sides, but less than their sum.


Complete Step by step Solution:
Given:
AC = BC
ABC is an isosceles triangle
 \[A{B^{2\;}} = {\text{ }}2{\text{ }}A{C^2}\]

To prove: ABC is a right angled triangle

Proof:

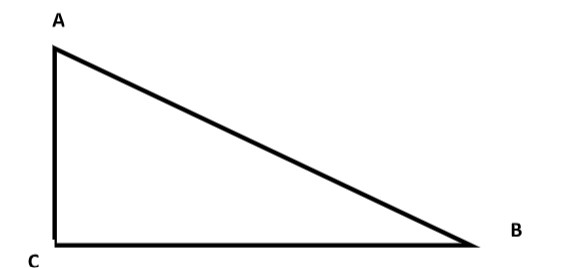
Consider a right angled triangle ABC as shown in the figure
For ABC to be a right triangle, it should satisfy Pythagoras theorem
i.e \[
  A{B^{2\;}} = {\text{ }}A{C^{2\;}} + {\text{ A}}{C^2} \\
   \\ \] \[A{B^{2\;}} = {\text{ }}A{C^{2\;}} + {\text{ }}B{C^2}\]
Now, AC = BC (given)………………(1)
On substitution, we find
\[ \Rightarrow \]\[A{B^{2\;}} = {\text{ }}2{\text{ }}A{C^2}\]
\[ \Rightarrow \]\[A{B^{2\;}} = {\text{ }}A{C^{2\;}} + {\text{ A}}{C^2}\]
\[ \Rightarrow \]\[A{B^{2\;}} = {\text{ }}A{C^{2\;}} + {\text{ }}B{C^2}\]
Here AB is the largest side ,i.e Hypotenuse of triangle ABC.
So, the given sides form Pythagorean triplets.
Hence ABC to be a right triangle right angled at C.


Note:Students should keep in mind the formula of Pythagoras theorem and its implementation on right angled triangles.