Question

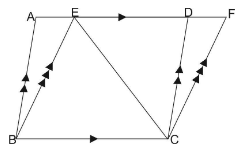
ABCD and BCEF are parallelograms. If area of $ \Delta EBC = 480c{m^2},\,\,AB = 30cm\,\,and\,\,BC = 40cm. $ Calculate area of parallelogram ABCD.

\[
  A.\,\,960c{m^2} \\
  B.\,\,860c{m^2} \\
  C.\,\,280c{m^2} \\
  D.\,\,130c{m^2} \\
  E.\,\,1960c{m^2} \\
 \]

Answer 1

Hint: In this problem we first find area of parallelogram BCFE from given area of triangle BCE and then using area of triangle we find height of triangle and then using this height we will find area of parallelogram ABCDE and hence the required solution of the problem .
Formulas used: Area of parallelogram = $ base \times altitude(height) $ , Area of triangle = $ \dfrac{1}{2} \times base \times height(altitude) $

Complete step by step solution:
It is given an area of triangle EBC = $ 480c{m^2} $ .

Also, triangle EBC is drawn on common base BC of parallelogram BCFE and diagonal EC divides parallelogram BCFE in two equal parts or areas.
Therefore, area of ||gm BCFE = $ 2 \times ar\left( {\Delta EBC} \right) $
 $
   \Rightarrow ar\left( {||gmBCFE} \right) = 2 \times 480 \\
   \Rightarrow ar\left( {||gmBCFE} \right) = 960 \\
  $
Hence, from above we see that area of ||gm(BCFE) is $ 960c{m^2} $ .

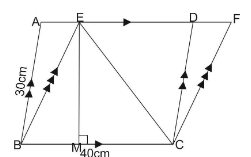
Also, we know that area of triangle BCE is given as: $ \dfrac{1}{2} \times BC \times height(EM) $
Substituting values in above we have,
 $
  480 = \dfrac{1}{2} \times 40 \times height \\
   \Rightarrow height = \dfrac{{480 \times 2}}{{40}} \\
   \Rightarrow heigth = 24 \;
  $
Therefore, height of triangle BCE or ||gm BCDA is $ 24cm. $
Therefore, area of ||gm BCDA is given as: $ base \times height $
Substituting values in above. We have
 $
  ar\left( {||gmBCDA} \right) = 40 \times 24 \\
   = 960c{m^2} \;
  $
Hence, from above we can say that area of parallelogram ABCD is $ 960c{m^2} $
So, the correct answer is “Option A”.

Note: We can also find the solution of a given problem by using the concept of theorem. In this we know that the area of two parallelograms are equal if they lie on the same base between parallel lines and the area of the triangle is half of the area of the parallelogram if the triangle and parallelogram have the same base and in between parallel lines. So, form this concept from the area of a given triangle we can easily find the area of one parallelogram and then form one parallelogram we can find the area of the other parallelogram and hence the required solution of the problem.