ABCD is a parallelogram in which angle $\angle A = {70^0}$ . Compute angle B,angle C and angle D.

Question

Vedantu Content Team · Accepted Answer

Hint: Use geometrical theorems related to parallel lines.
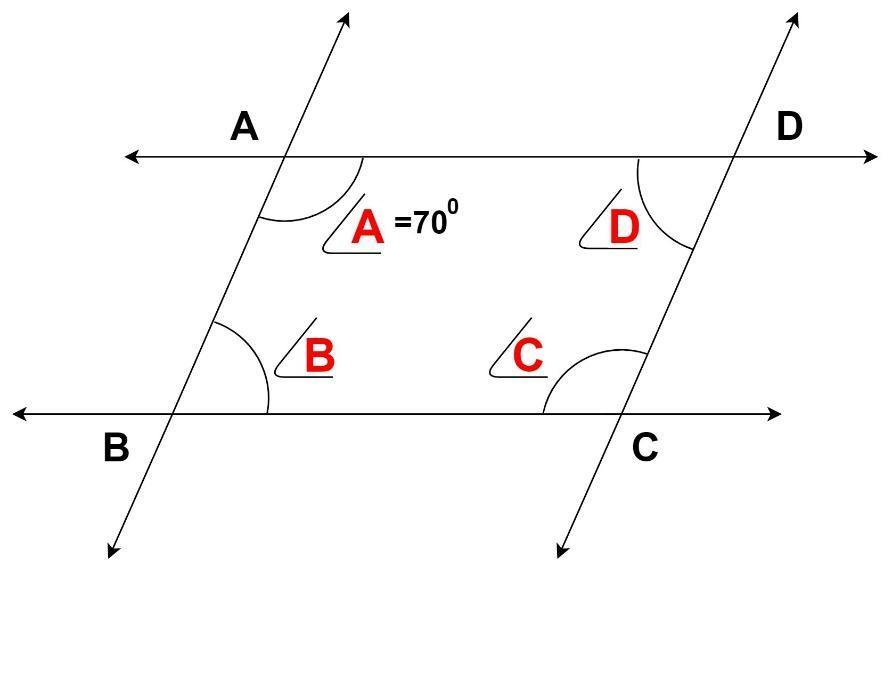
Given in the problem ABCD is a parallelogram with angle $\angle A = {70^0}$.
We know that opposite sides of the parallelogram are parallel to each other.
$
   \Rightarrow AB{\text{ is parallel to }}CD{\text{ (1)}} \\
   \Rightarrow AD{\text{ is parallel to B}}C{\text{ (2)}} \\
$
Same side Interior angle theorem states that the interior angles formed by a transversal line intersecting two parallel lines are supplementary.
Using the same theorem in parallelogram $ABCD$, we get:
\[
  (1) \Rightarrow {\text{ }}\angle A + \angle D = {180^0}{\text{ and }}\angle B + \angle C = {180^0} \\
  (2) \Rightarrow {\text{ }}\angle A + \angle B = {180^0}{\text{ and }}\angle C + \angle D = {180^0} \\
\]
Using angle $\angle A = {70^0}$ in above equations, we get:
  \[
  {70^0} + \angle D = {180^0}{\text{ }} \\
   \Rightarrow \angle D = {110^0} \\
  {70^0} + \angle B = {180^0} \\
   \Rightarrow \angle B = {110^0} \\
  \angle B + \angle C = {180^0} \\
   \Rightarrow \angle C = {70^0} \\
\]
Hence\[{\text{ }}\angle B = {110^0}{\text{ , }}\angle C = {70^0}{\text{ , }}\angle D = {110^0}\] .

Note: The same side interior angle theorem is only valid for parallel lines. Geometric properties of parallelogram and parallel lines should be kept in mind while solving problems like this.

ABCD is a parallelogram in which angle $\angle A = {70^0}$ . Compute angle B,angle C and angle D.

NCERT Book Solutions

Reference Book Solutions

Question Papers

Exams

Quick Links

ABCD is a parallelogram in which angle $\angle A = {70^0}$ . Compute angle B,angle C and angle D.

Book your FREE Online counselling session

Your FREE Online counselling session has been booked!

Please try again later

NCERT Book Solutions

Reference Book Solutions

Question Papers

Exams

Quick Links