Question

ABCD is a parallelogram. The sides AB and AD are produced to E and F respectively, such that AB=BE and AD=DF.
Hence, \[\Delta BEC\cong \Delta DCF\]
If the above statement is true then mention the answer as \[1\], else mention \[0\] if false.

Answer 1

Hint: From the question we have been given a statement and we are asked whether the statement is true or false. For solving this question we will take the help of side angle side rule or simply SAS rule in mathematics and see whether the \[\Delta BEC\cong \Delta DCF\] is true or false. So, we proceed with the solution as follows.

Complete step by step solution:
The figure will be as follows.

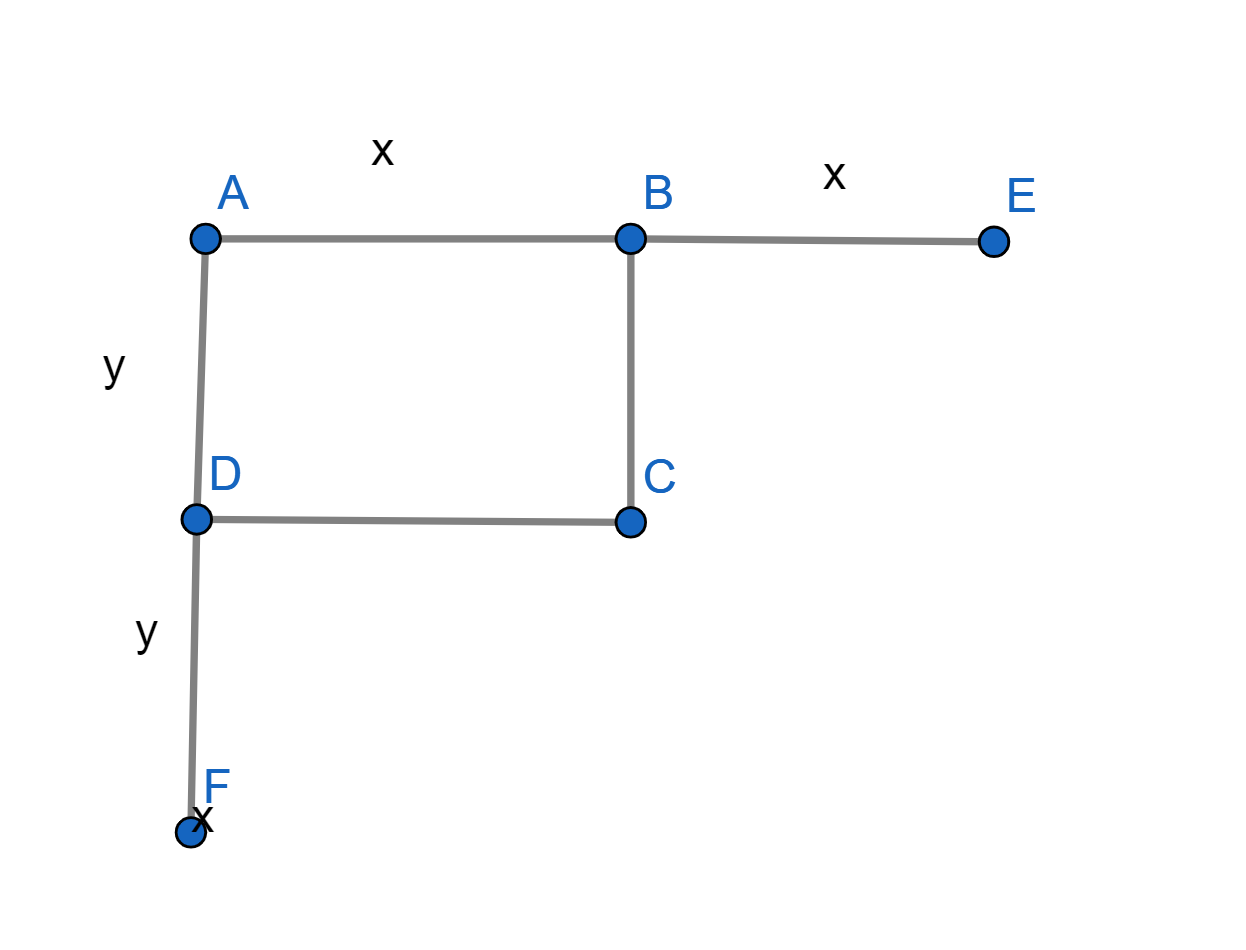
Corresponding angles for parallel lines AB and CD
\[\Rightarrow \angle BAD=\angle CDF\]
Corresponding angles for parallel lines AB and CD
\[\Rightarrow \angle BAD=\angle CBE\]
Thus, \[\Rightarrow \angle CDF=\angle CBE...........(1)\]
We are given that ABCD is a parallelogram so we know that,
\[\Rightarrow AD=BC\]
We are given,
\[\Rightarrow AD=DF\]
\[\therefore DF=BC............(2)\]
In the similar way we get as follows.
\[\therefore BE=CD............(3)\]
Now, consider angles by CDF and CBE.
From the help of equation \[(1)\],
\[\Rightarrow \angle CDF=\angle CBE\]
From equation \[(2)\]
\[\Rightarrow FD=BC\]
From equation \[(3)\]
\[\Rightarrow BE=CD\]
Thus from the side angle side rule that is SAS rule, we get,
\[\Rightarrow \Delta FDC\cong \Delta CBE\]
\[\Rightarrow \Delta BEC\cong \Delta DCF\]
Therefore, the statement given is true.

Note: Students should have good knowledge in the concept of sides and angles of parallelogram. Students should have good knowledge in the SAS rule and its applications to solve these kinds of questions.