Question

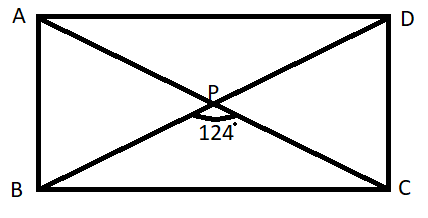
ABCD is a rectangle if $\angle BPC = {124^o}$ Calculate: $\angle BAP{\text{ and }}\angle ADP$.

Answer 1

Hint: In this particular question use the concept that the adjacent sides of the rectangle always makes a 90 degrees and the diagonals of the rectangle are always equal and also bisect each other so use these concepts to reach the solution of the question.

Complete step by step answer:
Given data:
$\angle BPC = {124^o}$................. (1)
Now as we see from the figure that APC is the diagonal of the rectangle which is a straight line so it makes a straight angle with the point p.
Now as we know that the straight angle = 180 degrees.
So, $\angle BPC + \angle BPA = {180^o}$
Now from equation (1) we have,
$ \Rightarrow {124^o} + \angle BPA = {180^o}$
$ \Rightarrow \angle BPA = {180^o} - {124^o} = {56^o}$............ (2)
Now as we know that in a rectangle the length of the diagonals are always equal and also bisect each other.
Therefore, PA = PB = PC = PB.
So triangles ABP, BCP, CDP, and DAP are an isosceles triangle.
Now as we know that in a isosceles triangle angles opposite to equal sides are always equal.
So in triangle ABP, as AP = BP, so $\angle PBA = \angle BAP$.............. (3)
Now as we know that in a triangle the sum of all angles are equal to 180 degrees.
So in triangle ABP we have,
$ \Rightarrow \angle PBA + \angle BAP + \angle BPA = {180^o}$
Now from equation (2) and (3) we have,
$ \Rightarrow \angle BAP + \angle BAP + {56^o} = {180^o}$
$ \Rightarrow \angle BAP = \dfrac{{{{180}^o} - {{56}^o}}}{2}$
$ \Rightarrow \angle BAP = \dfrac{{{{124}^o}}}{2} = {62^o}$
$ \Rightarrow \angle PBA = \angle BAP = {62^o}$
Now as we know in a rectangle opposite sides are equal and parallel to each other.
Therefore, $\angle PBA = \angle PDC = {62^o}$............. (4) (alternate angles)
Now as we know that in a rectangle adjacent sides of the rectangle always makes a 90 degrees.
Therefore, $\angle ADC = {90^o}$
$ \Rightarrow \angle ADP + \angle PDC = {90^o}$
Now from equation (4) we have,
$ \Rightarrow \angle ADP + {62^o} = {90^o}$
$ \Rightarrow \angle ADP = {90^o} - {62^o} = {28^o}$

So, the correct answer is “${28^o}$”.

Note: Whenever we face such types of questions the key concept we have to remember is that always recall all the properties of rectangle and isosceles triangle which is stated above and always recall that if a line join end points of a two parallel lines then the opposite angle create by this line is always equal and are called as alternate angles.