Question

ABCD is a rectangle in which diagonal AC bisects $\angle A$as well as $\angle C$. Show that,
(I) ABCD is square (ii) diagonal BD bisects $\angle B$ as well as $\angle D$.

Answer 1

Hint: - Here we go through by first making the diagram of the rectangle as the question says in which the diagonal AC bisect the $\angle A$ and $\angle C$. And then apply the properties of triangles to prove the question.

Complete step-by-step solution -
Here in the question it is given that,
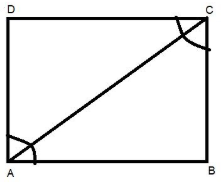
ABCD is a rectangle, in which diagonal AC bisects $\angle A$as well as $\angle C$.
So first we make the diagram of the rectangle showing the above statement. By the diagram we can say that,
$\angle DAC = \angle CAB$………….. (1)
$\angle DCA = \angle BCA$………….. (2)
We know that a square is a rectangle when all sides are equal. Now,
From diagram we can see, $AD\parallel BC$ and AC is transversal of the parallel lines therefore we can say that
$\angle DAC = \angle BCA$ (Alternate interior angles).
From (1), $\angle CAB = \angle BCA$……. (3)
Now in $\vartriangle ABC$
$\angle CAB = \angle BCA$ (As we proved above).
So we can say BC=AB ……. (4) (As we know the sides opposite to equal angles are equal).
But BC=AD and AB=DC …….. (5) (We know that the opposite sides of rectangles are equal).
Therefore from (4) & (5),
AB=BC=CD=AD and we know that in the rectangle all the interior angles are ${90^0}$. So we can say that ABCD is a square.
Hence, ABCD is a square.
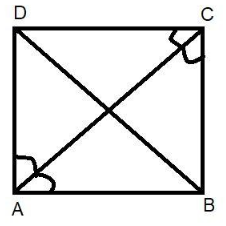
And in (ii) we have to prove diagonal BD bisects $\angle B$ as well as $\angle D$.
As we know from the properties of squares that the diagonals of a square bisect the angles into two equal parts. So we can say that the diagonals BD bisects the $\angle B$ as well as $\angle D$.
Hence, diagonal BD bisects $\angle B$ as well as $\angle D$.

Note: - Whenever we face such a type of question the key concept for solving the question is first of all make the diagrams as per the statement of question and then define what is given in the question. And then for proving the question, approach our results in the manner that we have to prove. Here we have to prove the square so we have to approach in the manner such that we can prove all the sides are equal to prove the square.