Question

ABCD is a rectangle whose three vertices are \[B(4,0)\], \[C(4,3)\] and \[D(0,3)\]. The length of one of its diagonals is
A. \[5\]
B. \[4\]
C. \[3\]
D. \[25\]

Answer 1

Hint: Here we draw a diagram of the rectangle ABCD with given vertices \[B(4,0)\], \[C(4,3)\] and \[D(0,3)\].
We join the diagonals and find the length of the diagonal whose both endpoints are given to us using the formula of length of a line segment.
* Length of a line segment joining points \[X(a,b),Y(c,d)\] is given by \[\sqrt {{{(a - c)}^2} + {{(b - d)}^2}} \].

Complete step-by-step answer:
We draw a rectangle ABCD with given vertices \[B(4,0)\], \[C(4,3)\] and \[D(0,3)\].

               

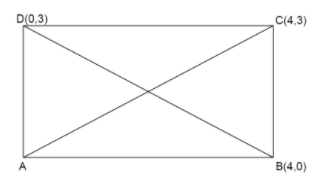
Now we see the diagonals are AC and BD.
But, the diagonal whose both end points are given in the figure is BD.
BD has endpoints \[B(4,0)\] and \[D(0,3)\]
Now from the formula of length of a line segment joining two points \[X(a,b),Y(c,d)\] is given by \[\sqrt {{{(a - c)}^2} + {{(b - d)}^2}} \].
On comparing the points we get \[a = 4,b = 0,c = 0,d = 3\]
Therefore, the length \[BD = \sqrt {{{(4 - 0)}^2} + {{(0 - 3)}^2}} \]
Solve the value under the root.
\[ \Rightarrow BD = \sqrt {{{(4)}^2} + {{( - 3)}^2}} \]
Square the terms in the bracket
\[
   \Rightarrow BD = \sqrt {16 + 9} \\
   \Rightarrow BD = \sqrt {25} \\
 \]
Now we can write the term under the root as \[25 = {5^2}\]
\[ \Rightarrow BD = \sqrt {{5^2}} \]
Cancel out the square power by square root.
\[ \Rightarrow BD = 5\]
So, the length of one of the diagonals of rectangle ABCD is 5 units.

So, the correct answer is “Option A”.

Note: Alternative method:
Since, the rectangle has all angles as right angles, so we take the right triangle BCD.
We find the lengths of sides BC and CD using the formula of line segment joining two points.
For line BC:
Points joining BC are \[B(4,0),C(4,3)\]
So, length \[BC = \sqrt {{{(4 - 4)}^2} + {{(0 - 3)}^2}} \]
\[
   \Rightarrow BC = \sqrt {{0^2} + {{( - 3)}^2}} \\
   \Rightarrow BC = \sqrt {{3^2}} \\
 \]
Cancel square root by square power.
\[ \Rightarrow BC = 3\]
For line CD:
Points joining BC are \[C(4,3)\], \[D(0,3)\]
So, length \[CD = \sqrt {{{(4 - 0)}^2} + {{(3 - 3)}^2}} \]
\[
   \Rightarrow CD = \sqrt {{4^2} + {0^2}} \\
   \Rightarrow CD = \sqrt {{4^2}} \\
 \]
Cancel square root by square power.
\[ \Rightarrow CD = 4\]
We know that in a right angled triangle, Pythagoras theorem states that the square of the hypotenuse is equal to sum of square of base and perpendicular of the triangle.
So now applying Pythagoras theorem in \[\vartriangle BCD\] where \[\angle C = {90^ \circ }\]
\[B{D^2} = B{C^2} + C{D^2}\]
Substituting the values of \[BC = 3\], \[CD = 4\]
\[
   \Rightarrow B{D^2} = {(3)^2} + {(4)^2} \\
   \Rightarrow B{D^2} = 9 + 16 \\
   \Rightarrow B{D^2} = 25 \\
 \]
Now we write the term on right hand side in form of its multiples
\[ \Rightarrow B{D^2} = {5^2}\]
Take under root on both sides of the equation.
\[ \Rightarrow \sqrt {B{D^2}} = \sqrt {{5^2}} \]
Cancel under root by square power
\[ \Rightarrow BD = 5\]
So, the length of the diagonal BD is 5 units.
So, option A is correct.