Question

$ABCD$ is a rhombus. Show that diagonal $AC$ bisects $\angle A$ as well as $\angle C$ and diagonal $BD$ bisects $\angle B$ as well as $\angle D$.

Answer 1

Hint: All the sides of a rhombus are equal and the opposite sides are parallel to each other. Also, in a rhombus the angles opposite to equal sides are always equal.

Complete step by step solution:

The following is the schematic diagram of a rhombus.

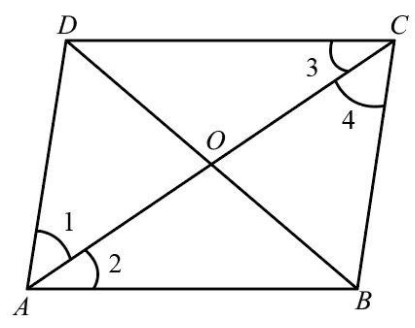
Consider $\Delta ABC$,
Since all the sides of rhombus are equal, therefore
$AB = BC$

The angles opposite to the sides $AB$ and $BC$ will be equal. hence
$\angle 4 = \angle 2$.….(i)

Also $AD\parallel BC$ with transversal $AC$, as $AD$ and $BC$ are opposite sides of rhombus and opposite sides of rhombus are parallel to each other. Hence alternate angles will be equal.
$\angle 1 = \angle 4$……(ii)

From equation (i) and (ii).
$\angle 1 = \angle 2$

Hence, it is clear that $AC$ bisects the angle $\angle A$.

Now $AB\parallel DC$ with transversal $AC$, as $AB$ and $DC$ are opposite sides of rhombus and opposite sides of rhombus are parallel to each other. Hence alternate angles will be equal.
$\angle 2 = \angle 3$……(iii)

From equation (i) and (iii).
$\angle 4 = \angle 3$

Hence, it is clear that $AC$ bisects the angle $\angle C$.

Therefore $AC$ bisects angles $\angle A$ and $\angle C$.

Since $CD$ and $BC$ are the sides of rhombus, therefore $CD = BC$.

The following is the schematic diagram of a rhombus.

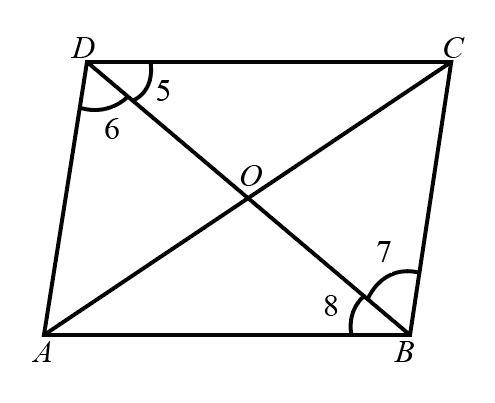
The angles opposite to the sides $CD$ and $BC$ will be equal. hence
$\angle 5 = \angle 7$..….(iv)

Also $AB\parallel CD$ with transversal $BD$ , as $AB$ and $CD$ are opposite sides of rhombus and opposite sides of rhombus are parallel to each other. Hence alternate angles will be equal.
$\angle 5 = \angle 8$……(v)

From equation (iv) and (v).
$\angle 7 = \angle 8$

Hence $BD$ bisects the angle $\angle B$.

Now $AD\parallel BC$ with transversal $BD$, as $AD$ and $BC$ are opposite sides of rhombus and opposite sides of rhombus are parallel to each other. Hence alternate angles will be equal.
$\angle 6 = \angle 7$……(vi)

From equation (v) and (vi).
$\angle 5 = \angle 6$

Hence $BD$ bisects the angle $\angle D$.

Therefore $BD$ bisects angles $\angle B$ and $\angle D$.

Note: Angle bisector divides the angle in two equal angles. Make sure to use the properties of rhombus in the solution.