
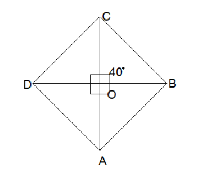
ABCD is a rhombus such that \[\angle \text{ACB}={{40}^{\circ }}\ then \\angle \text{ADB}\] is ?
A. \[{{40}^{\circ }}\]
B. \[{{50}^{\circ }}\]
C. \[{{45}^{\circ }}\]
D. None of these

Answer
552.6k+ views
Hint:To find the value of \[\angle \text{ADB}\], we first find the value of \[\angle \text{CBD}\] by using the formula of sum of all the angles equal to \[{{180}^{\circ }}\] and after finding the value of angle \[\angle \text{CBD}\], we use the alternative angle method where we find the value of \[\angle \text{ADB}\].
Complete step by step solution:
Let us draw the diagram and according to the diagram given, we will find the value of the angle \[\angle \text{CBD}\]. To find the \[\angle \text{CBD}\], we first check the triangle \[CBO\]which contains the angle \[\angle OCB\] and \[\angle COB\] i.e. \[{{40}^{\circ }}\] and \[{{90}^{\circ }}\] respectively.
Hence, the value of the angle \[\angle \text{CBD}\], we use the formula of the sum of the angle equal to \[{{180}^{\circ }}\] where we put the values in the formula as:
\[\Rightarrow \angle C+\angle O+\angle B={{180}^{\circ }}\]
\[\Rightarrow {{40}^{\circ }}+{{90}^{\circ }}+\angle B={{180}^{\circ }}\]
\[\Rightarrow \angle B={{180}^{\circ }}-{{130}^{\circ }}\]
\[\Rightarrow \angle B={{50}^{\circ }}\]
Now that we have the value of \[\angle B\], we can find the value of the \[\angle D\] by using the alternate angle method where the angle \[CBD\] and \[BDA\] are the same. Therefore, the value angle \[BDA\] is also given as \[{{50}^{\circ }}\].
Note: Rhombus like square have equal sides but the outer angles are not same hence, the outer angle of a rhombus can’t be deemed as \[{{90}^{\circ }}\] and similarly student may go wrong if they try to take the outer angles as \[{{90}^{\circ }}\] and start their questions with it.
Complete step by step solution:
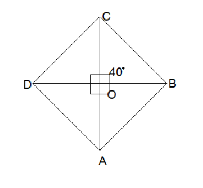
Let us draw the diagram and according to the diagram given, we will find the value of the angle \[\angle \text{CBD}\]. To find the \[\angle \text{CBD}\], we first check the triangle \[CBO\]which contains the angle \[\angle OCB\] and \[\angle COB\] i.e. \[{{40}^{\circ }}\] and \[{{90}^{\circ }}\] respectively.

Hence, the value of the angle \[\angle \text{CBD}\], we use the formula of the sum of the angle equal to \[{{180}^{\circ }}\] where we put the values in the formula as:
\[\Rightarrow \angle C+\angle O+\angle B={{180}^{\circ }}\]
\[\Rightarrow {{40}^{\circ }}+{{90}^{\circ }}+\angle B={{180}^{\circ }}\]
\[\Rightarrow \angle B={{180}^{\circ }}-{{130}^{\circ }}\]
\[\Rightarrow \angle B={{50}^{\circ }}\]
Now that we have the value of \[\angle B\], we can find the value of the \[\angle D\] by using the alternate angle method where the angle \[CBD\] and \[BDA\] are the same. Therefore, the value angle \[BDA\] is also given as \[{{50}^{\circ }}\].
Note: Rhombus like square have equal sides but the outer angles are not same hence, the outer angle of a rhombus can’t be deemed as \[{{90}^{\circ }}\] and similarly student may go wrong if they try to take the outer angles as \[{{90}^{\circ }}\] and start their questions with it.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




