Question

ABCD is a rhombus whose diagonals intersect at E. Then \[\overrightarrow{EA}+\overrightarrow{EB}+\overrightarrow{EC}+\overrightarrow{ED}\] equals
A. \[\overrightarrow{0}\]
B. \[\overrightarrow{AD}\]
C. \[2\overrightarrow{BC}\]
D. $2\overrightarrow{AD}$

Answer 1

Hint: We will start by using a fact that all the sides of a rhombus are equal and the diagonal bisect each other at right. Then, we will use the fact that if two vectors are the same in magnitude but different in direction then their resultant is zero and finally we will use this fact of the rhombus to make pair of vectors and solve them.

Complete step-by-step solution -
Now, we have been given that ABCD is a rhombus whose diagonals intersect at E and we have to find the value of \[\overrightarrow{EA}+\overrightarrow{EB}+\overrightarrow{EC}+\overrightarrow{ED}\].

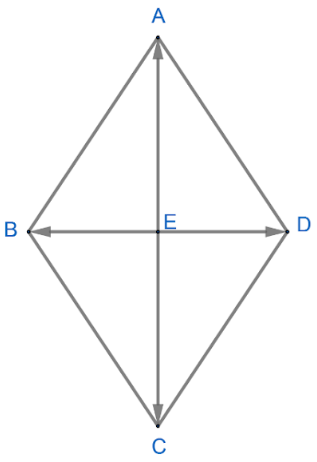
Now, we know that the diagonals of a parallelogram are perpendicular and bisect each other, so we have,
$\begin{align}
  & EA=EC...............\left( 1 \right) \\
 & EB=ED................\left( 2 \right) \\
\end{align}$
Now, we know that if two vectors which are same in magnitude but opposite in direction are added their resultant is zero. Therefore, we have from (1) and (2),
$\begin{align}
  & \overrightarrow{EA}+\overrightarrow{EC}=0...............\left( 3 \right) \\
 & \overrightarrow{EB}+\overrightarrow{ED}=0...............\left( 4 \right) \\
\end{align}$
Now, adding (3) and (4) we have;
\[\overrightarrow{EA}+\overrightarrow{EB}+\overrightarrow{EC}+\overrightarrow{ED}=0\]
Hence, the correct option is A.

Note: It is important to note that we have used the property of rhombus and diagonals of a rhombus bisect each other. So, we have used this and another fact that the sum of two equal and the opposite vector is zero to find the solution to the question.