Question

ABCD is quadrilateral in which $AD=BC$. If P,Q,R,S be the mid-points of AB, AC, CD and BD respectively, show that PQRS is a rhombus.

Answer 1

Hint: Draw a neat diagram with the help of given information in the quadrilateral ABCD. Use the mid-point theorem of a triangle which can be given as :-
Line joining the mid-points of two sides of the triangle will be parallel to the third side of the triangle and half of it as well. Rhombus is a parallel organ with equal sides.

Complete step-by-step answer:
Information provided in the problem are
(i) ABCD is a quadrilateral with condition $AD=BC$
(ii) P,Q,R,S are mid-points of AB, AC, CD,BD.
And hence, we need to show that PQRS is a rhombus.
So, we can draw diagram with the help of above information as

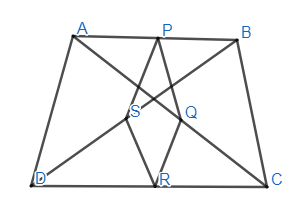
So, we have
$AD=BC$ (i)
$AP=BP=\dfrac{AB}{2}$ (ii)
$BS=SD=\dfrac{BD}{2}$ (iii)
$DR=RC=\dfrac{DC}{2}$ (iv)
$AQ=QC=\dfrac{AC}{2}$ (v)
Where, equations (ii), (iii), (iv), (v) are written with the help of second information in the problem i.e. P, Q, R, S are mid-points of AB, AC, CD, BD.
As we know, the mid-point theorem states that a line joining midpoints of any two sides of a triangle will be parallel to the third side of the triangle and half of the length of the third side. So, we can apply mid-point theorem in triangle ADB, and where P and S are mid-points of AB and BD, So, we get
$PS\parallel AD$ and $PS=\dfrac{AD}{2}$ (vi)
Similarly, applying mid-point theorem in triangles BCD, ABC, ACD and get respectively as
$SR\parallel BC$ and $SR=\dfrac{BC}{2}$ (vii)
$PQ\parallel BC$ and $PQ=\dfrac{BC}{2}$ (viii)
$QR\parallel AD$ and $QR=\dfrac{AD}{2}$ (ix)
Now, from equation (vi) and (ix), we get
$PS\parallel QR\parallel AD$ and $PS=QR=AD$ (x)
And from equation (vii) and (viii) we get
$SR\parallel PQ\parallel BC$ and $SR=PQ=\dfrac{BC}{2}$ (xi)
As, we know parallelogram has equal and parallel opposite sides, so, we can get from above equations in quadrilateral PQRS that
$PS\parallel QR$ and $PS=QR$
and $SR\parallel PQ$ and $SR=PQ$
Hence, PQRS is a Parallelogram.
Now, it is given that $AD=BC$ from equation (i) and so, we can get from equation (x), (xi) and (i) as
$PS=QR=\dfrac{AD}{2}$ and $SR=PQ=\dfrac{BC}{2}$
$\Rightarrow 2PS=2QR=AD$ and $2SR=2PQ=BC$
As; $AD=BC$ , So we get
$\begin{align}
  & 2PS=2QR=AD=2SR=2PQ=BC \\
 & \Rightarrow 2PS=2QR=2SR=2PQ \\
\end{align}$
$\Rightarrow PS=QR=SR=PQ$ (xii)
Hence, as we know rhombus has equal four sides and parallel opposite sides. So, we can get from equation (xii) that parallelogram PQRS is rhombus as all four sides or it are equal
Hence, PQRS is a rhombus.

Note: Solve these kinds of questions by writing all the information provided in the problem and try to relate theorems with respect to given information as information will act as a hint of these types of questions. Drawing a diagram with the help of information provided and applying mid-point theorem are the key points of the problem. Using any theorem makes our problem easier and flexible.