Question

What is the acceleration of the block and trolley as shown in figure? If the coefficient of kinetic friction between the trolley and surface is $0.04$? What is the tension in the string? (Take $g = 10m{s^{ - 2}}$). Neglect the mass of the string.

Answer 1

Hint: Here given in the question the data of weight of a trolley and net weight of the block as shown in the figure. For this given data there is applied and kinetic friction in between the trolley and block with a tension of spring here we have to neglect the mass of the string. For this calculation we are using the kinetic friction formula.

Complete step by step answer:
Force is equal to change in velocity to change in time. Force is equal to product of mass and acceleration whereas the friction of force depends on the mass of an object and coefficient of the sliding friction between them. For finding the acceleration of an object we have to subtract the force from the applied force.

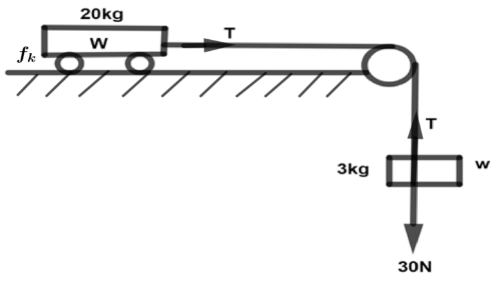
Given data of kinetic coefficient friction is $0.04$.
Given masses of the trolley and block is ${m_1}$ and ${m_2}$,
Kinetic coefficient of friction $\left( {{\mu _k} = 0.04} \right)$
From this we are assuming the equation in two cases,
In first case, $30 - T = {m_1}a \to \left( 1 \right)$
Here ${m_1} = 3kg$
So equation (1) written as, $30 - T = 3 \times a \to \left( 2 \right)$
In second case, $T - {f_k} = {m_2}a \to \left( 3 \right)$
Here we are finding the value of ${f_k} = {\mu _k}R$ then,
$R = {m_2}g \\
\Rightarrow R = 20 \times g \\ $
Here $g = 10$
By adding g value in R we get,
$R = 20 \times 10 \\
\Rightarrow R = 200N \\ $
Here we are calculating,
${f_k} = 0.04 \times 200 \\
\Rightarrow {f_k} = 8N \\ $
Then in second case we get,
By adding equations (2) and (4), we get,
$30 - T + T - 8 = 3 \times a + 20 \times a \\
\Rightarrow 22 = 23a \\
\therefore a = \dfrac{{22}}{{23}} \\ $
Here approximately $a$ value is, $a = 0.956m{s^{ - 2}}$.
Now we are calculating the tension of the string,
$T = 20 \times a + 8 \\
\Rightarrow T = 20 \times 0.956 + 8 \\
\therefore T = 27.1\,N $

Hence,the acceleration of the block and trolley is $\dfrac{{22}}{{23}}\,m/{s^2}$ and the tension in the string is 27.1 N.

Note: in the above solution part we have discussed the kinetic coefficient friction of trolley and blocks. For this calculation we have used a formula of acceleration from this we have calculated the tension of the string while neglecting the mass of the string. The tension of string value is, $T = 27.1\,N$.