
AD is a median of the triangle ABC and E is the midpoint of AD. BE produced meets AC in F, prove that
Answer
532.5k+ views
Hint: First of all, draw the diagram to get a clear idea of the question. Now construct DG || BF through D. Then take triangles
Complete step-by-step answer:
Here, we are given that AD is the median of the triangle ABC, and E is the midpoint of AD. BE produced meets AC at F. We have to prove that
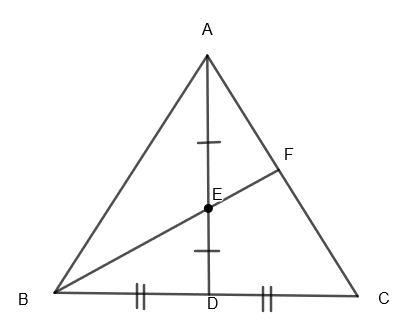
In the above figure, AD is the median of the triangle, therefore, we get, BD = DC …..(i)
Also, E is the midpoint of AD, therefore, we get AE = ED …..(ii)
Here, BE is produced such that it meets AC at F. Now let us construct a line DG parallel to BF through D as follows:
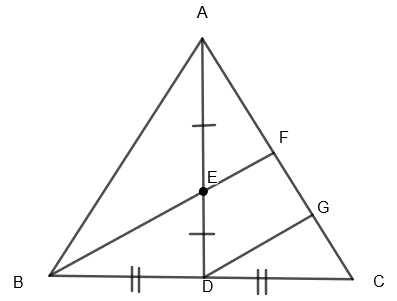
We know that the converse of the midpoint theorem states that “If a line is drawn through the midpoint of one side of a triangle and parallel to other sides, it bisects the third side or the point at which it meets the third side is the midpoint of the third side”.
In
Also, in
From equation (iii) and (iv), we get, AF = FG = GC ……(v)
Now, from the diagram, AF + FG + GC = AC
By substituting FG = AF and GC = AF from equation (v), we get, AF + AF + AF = AC.
3 AF = AC
By dividing 3 on both the sides of the above equation, we get,
Hence proved.
Note: Students must remember the midpoint theorem and its converse properly as it is one of the most important theorems of geometry. Also, in this question, students make mistakes in taking the different triangles to prove the result. So take the triangles which have the sides which are present in the final result to get the desired answer or to prove the desired result.
Complete step-by-step answer:
Here, we are given that AD is the median of the triangle ABC, and E is the midpoint of AD. BE produced meets AC at F. We have to prove that

In the above figure, AD is the median of the triangle, therefore, we get, BD = DC …..(i)
Also, E is the midpoint of AD, therefore, we get AE = ED …..(ii)
Here, BE is produced such that it meets AC at F. Now let us construct a line DG parallel to BF through D as follows:

We know that the converse of the midpoint theorem states that “If a line is drawn through the midpoint of one side of a triangle and parallel to other sides, it bisects the third side or the point at which it meets the third side is the midpoint of the third side”.
In
Also, in
From equation (iii) and (iv), we get, AF = FG = GC ……(v)
Now, from the diagram, AF + FG + GC = AC
By substituting FG = AF and GC = AF from equation (v), we get, AF + AF + AF = AC.
3 AF = AC
By dividing 3 on both the sides of the above equation, we get,
Hence proved.
Note: Students must remember the midpoint theorem and its converse properly as it is one of the most important theorems of geometry. Also, in this question, students make mistakes in taking the different triangles to prove the result. So take the triangles which have the sides which are present in the final result to get the desired answer or to prove the desired result.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the full form of POSCO class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

How do you prove that the diagonals of a rectangle class 10 maths CBSE




