Question

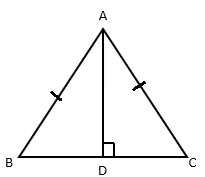
AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that (i) AD bisects BC (ii) AD bisects angle A.

Answer 1

Hint: CPCT stands for Corresponding Parts of Congruent Triangles. CPCT theorem states that if two or more triangles which are congruent to each other are taken then the corresponding angles and the sides of the triangles are also congruent to each other.Using this concept we shall prove the following statements.

Complete step by step answer:
Given that,
The triangle ABC is an isosceles triangle, So AB = AC
Also, AD is the altitude, so $\angle ADC=\angle ADB={{90}^{0}}$
To Prove that (i) BD =CD (ii) $\angle BAD=\angle CAD$
The proof are given below
In $\Delta ADB$ and$\Delta ADC$,
$\angle ADC=\angle ADB={{90}^{0}}$ (Both the angles are ${{90}^{0}}$, because AD is an altitude)
AB = AC (It is given.)
AD = AD (It is a common side)
By using the RHS congruence rule. The RHS theorem states that in two right-angled triangles, if the length of the hypotenuse and one side of one triangle is equal to the length of the hypotenuse and one side of the other triangle, then the two triangles are congruent.
Therefore, $\Delta ADB\cong \Delta ADC$
By for corresponding parts of congruent triangles (CPCT) theorem,
BD = DC and $\angle BAD=\angle CAD$
Hence, AD bisects BC and AD bisects angle A.

Note: You might get confused between RHS and SAS. The main difference between RHS and SAS is that RHS is applicable only in right angled triangles whereas SAS can be applicable to any given triangle. In RHS the angle is always of measure 90º whereas in SAS the angle is always the included angle between two sides