Question

Adjacent sides of a rectangle are $7 \mathrm{~cm}$ and $24 \mathrm{~cm}$. Find the length of its diagonal.

Answer 1

Hint: In geometry, a diagonal is a line segment joining two vertices of a polygon or polyhedron, when those vertices are not on the same edge. Informally, any sloping line is called diagonal. The definition of diagonal is something with slanted lines or a line that connects one corner with the corner furthest away. An example of diagonal is a line going from the bottom left corner of a square to the top right corner.
We can find the diagonal of a rectangle if we have the width and the height. The diagonal equals the square root of the width squared plus the height squared.

Complete step-by-step answer:
We can find the diagonal of a rectangle if we have the width and the height. The diagonal equals the square root of the width squared plus the height squared.
Let ABCD be a rectangle.

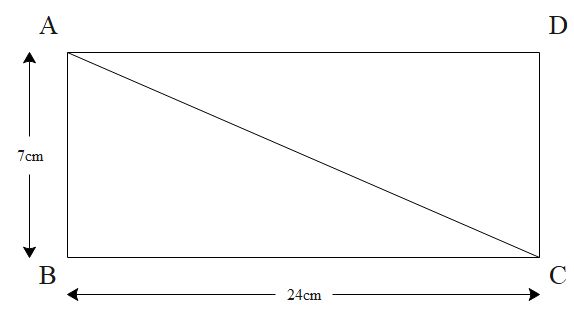
In $\triangle \mathrm{ABC}$
Angle $B=90^{\circ}$
$\mathrm{AC}^{2}=\mathrm{AB}^{2}+\mathrm{BC}^{2} \ldots$ Pythagoras theorem
$=7^{2}+24^{2}$
$=49+576$
$=625$
$A C=\sqrt{625} $
$A C=25 \mathrm{~cm}$
The length of the diagonal is $25 \mathrm{~cm}$.

Note: A diagonal is a straight line connecting the opposite corners of a polygon through its vertex. To learn about diagonals, we must first know that: It (diagonal) is a line segment. A parallelogram is a quadrilateral whose opposite sides are parallel and equal. The opposite sides being parallel and equal, forms equal angles on the opposite sides. Diagonals of a parallelogram are the segments which connect the opposite corners of the figure.