
A-line passing through origin and is perpendicular to two given lines
(a) 1:2
(b) 2:1
(c) 4:2
(d) 4:3
Answer
476.1k+ views
Hint: We start solving the problem by drawing the figure representing the given information. We then recall the fact that the perpendicular distance from the point
Complete step by step answer:
According to the problem, we are given that a line passing through the origin and is perpendicular to two given lines
Let us draw the figure representing the given information.
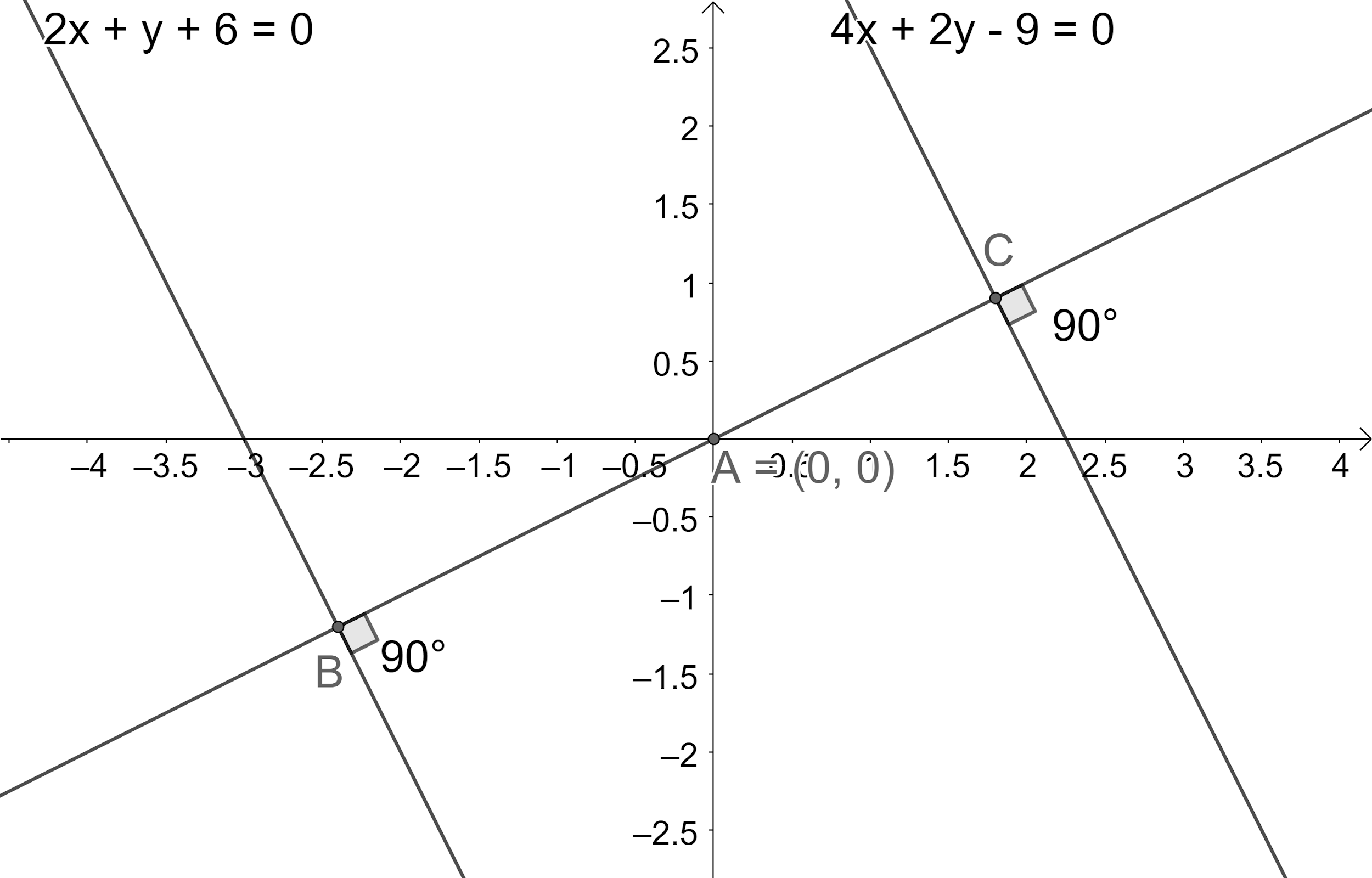
From the figure, we can see that we need to find the ratio of AB to AC.
We can see that AB and AC are the perpendicular distances from the point
We know that the perpendicular distance from the point
Now, we get
Now, we get
Now, let us take the ratio of AB to AC using the obtained values from equations (1) and (2).
So, we have
So, we have found the ratio that origin divides the line as 4:3.
Note:
We should perform each step carefully in order to avoid confusion and calculation mistakes. We can also solve this problem by finding the equation of the line passing through the origin and then finding the intersection points and then finding the distance between those points and the origin. Similarly, we can expect problems to find the perpendicular distance between the given parallel lines.
Complete step by step answer:
According to the problem, we are given that a line passing through the origin and is perpendicular to two given lines
Let us draw the figure representing the given information.

From the figure, we can see that we need to find the ratio of AB to AC.
We can see that AB and AC are the perpendicular distances from the point
We know that the perpendicular distance from the point
Now, we get
Now, we get
Now, let us take the ratio of AB to AC using the obtained values from equations (1) and (2).
So, we have
So, we have found the ratio that origin divides the line as 4:3.
Note:
We should perform each step carefully in order to avoid confusion and calculation mistakes. We can also solve this problem by finding the equation of the line passing through the origin and then finding the intersection points and then finding the distance between those points and the origin. Similarly, we can expect problems to find the perpendicular distance between the given parallel lines.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

What are the public facilities provided by the government? Also explain each facility




