
How many altitudes does a triangle have?
Answer
433.5k+ views
Hint: In the above problem, we are asked to find the number of altitudes that a triangle has. So, the number of possible altitudes can be seen as a triangle that has three vertices and three opposite sides with respect to those three vertices. And we know that altitude is a line segment from any vertex to the opposite side in such a way so that the line segment will make a right angle with the opposite vertex. In this way, you can draw the altitudes on a triangle and then count those altitudes.
Complete step-by-step solution:
Let us draw a triangle first. So, below, we have drawn a triangle ABC as follows:
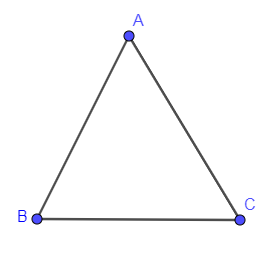
Now, we are asked to find the altitudes on this triangle. For that, we should know how altitudes are drawn inside the triangle. An altitude is drawn from any of the three vertices of a triangle onto the opposite side of the triangle and the angle that altitude is making with the opposite side is
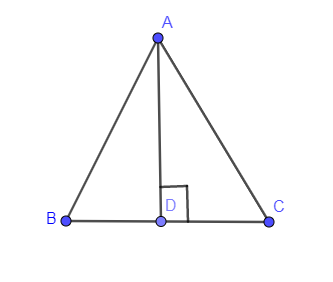
From the above figure, you can see that we have drawn AD on the side BC and AD is the altitude. Similarly, we are drawing altitudes from the vertices B and C we get,
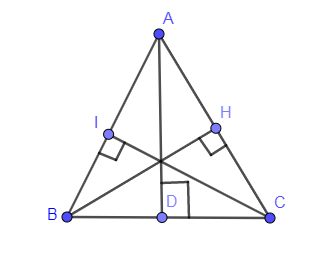
In the above figure, we have drawn two other altitudes BH and CI. Hence, a total of 3 altitudes are possible in the above triangle.
Hence, in a triangle a total of 3 altitudes are possible.
Note: An important point that we are sharing here is that the intersection point of the three altitudes is the orthocenter of the triangle is known as the orthocenter of the triangle. In geometry, you can find various problems related to the orthocenter so this is information which you will find in numerous applications.
Complete step-by-step solution:
Let us draw a triangle first. So, below, we have drawn a triangle ABC as follows:

Now, we are asked to find the altitudes on this triangle. For that, we should know how altitudes are drawn inside the triangle. An altitude is drawn from any of the three vertices of a triangle onto the opposite side of the triangle and the angle that altitude is making with the opposite side is

From the above figure, you can see that we have drawn AD on the side BC and AD is the altitude. Similarly, we are drawing altitudes from the vertices B and C we get,

In the above figure, we have drawn two other altitudes BH and CI. Hence, a total of 3 altitudes are possible in the above triangle.
Hence, in a triangle a total of 3 altitudes are possible.
Note: An important point that we are sharing here is that the intersection point of the three altitudes is the orthocenter of the triangle is known as the orthocenter of the triangle. In geometry, you can find various problems related to the orthocenter so this is information which you will find in numerous applications.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

What are the public facilities provided by the government? Also explain each facility




