Question

Altitudes meet at the vertex, so the orthocenter is located on the ----- of the right triangle.
(A) inside
(B) outer
(C) vertex
(D) away

Answer 1

Hint:To know the answer of this question we need to know what the orthocenter is. In this question we have to find the orthocenter in the right angled triangle. One should know about the terms of concurrent triangles as the orthocenter asked in the question. Orthocenter is the point in which altitudes intersect. In the right angled triangle all three altitudes meet at the inside triangle at a point.

Complete step-by-step answer:

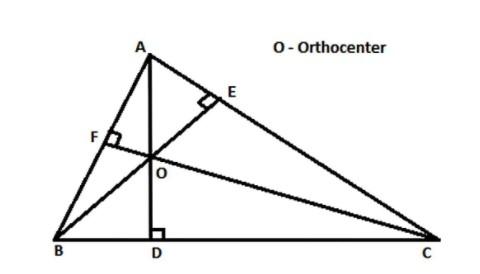
In the above diagram , in triangle ABC , AD , BE & CF are the altitudes at sides BC , AC & AB respectively & they meet at a point O inside the triangle . Hence point O is orthocenter in this figure .
In a right angled triangle, two sides i.e., base and perpendicular meet at right angle to one another, So, the altitudes of these sides meet at vertex where right angle is present. Angle, the perpendicular on altitude, drawn from hypotenuse meet other two altitudes on vertex again. As we know, orthocenter is a point of meeting of three altitudes inside the triangle.
The orthocenter is located on the vertex on the right-angled triangle.

So, the correct answer is “Option C”.

Note:In this question, there is a high chance of getting confused between the term Orthocenter, Centroid, Incentre & Circumcenter.Centroid is a point in which all the medians of a triangle meet whereas Orthocenter is a point in which all the three altitudes of a triangle meet.Incentre is a point where the bisector of all three angles of a triangle meets whereas Circumcenter is a point where all three bisectors of three sides of triangles meet.Students should remember these all definitions for solving these types of questions.