Question

An AC voltage source $V = {V_o}\sin \omega t$ is connected across resistance R and capacitance C as shown in the figure. It is given that the$R = \dfrac{1}{{\omega C}}$and the peak current is${I_o}$. If the angular frequency of the voltage source is changed to $\dfrac{\omega }{{\sqrt 3 }}$ then the new peak current in the circuit is,

A) $\dfrac{{{I_o}}}{2}$
B) $\dfrac{{{I_o}}}{{\sqrt 2 }}$
C) $\dfrac{{{I_o}}}{{\sqrt 3 }}$
D) $\dfrac{{{I_o}}}{3}$

Answer 1

Hint: The hurdles in the flow of current in due to the inductor or capacitor is the resistance due to the element. The resistance of the inductor or capacitor is known as reactance. We can calculate the total resistance of the circuit by considering the value of the resistance due to all the elements in the circuit.

Complete step by step answer:
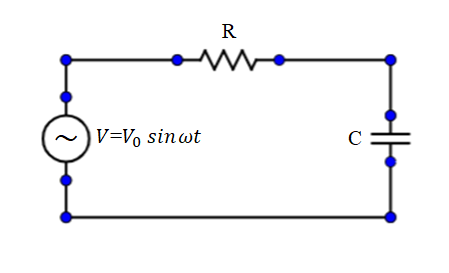
As it is given that capacitive reactance is given by $R = {{\text{X}}_C} = \dfrac{1}{{\omega C}}$ where C is the capacitance and $\omega $ is angular frequency. Let us calculate the total value of resistance.
$ \Rightarrow z = \sqrt {{R^2} + {{\left( {{{\text{X}}_c}} \right)}^2}} $
$ \Rightarrow z = \sqrt {{R^2} + {{\left( R \right)}^2}} $
$ \Rightarrow z = \sqrt 2 R$
As we know that, ${V_o} = Z \cdot {I_o}$ so the current is equal to,
$ \Rightarrow {I_o} = \dfrac{{{V_o}}}{Z}$
$ \Rightarrow {I_o} = \dfrac{{{V_o}}}{{\sqrt 2 R}}$………eq. (1)
As the$\omega $ becomes$\dfrac{1}{{\sqrt 3 }}$ the resistance will become$\sqrt 3 R$.
So the new resistance resultant will be,
$ \Rightarrow Z' = \sqrt {{R^2} + {{\left( {\sqrt 3 R} \right)}^2}} $
$ \Rightarrow Z' = \sqrt {4{R^2}} $
$ \Rightarrow Z' = 2R$
So the new peak current is equal to,
$ \Rightarrow {I_o}^\prime = \dfrac{{{V_o}}}{{Z'}}$
$ \Rightarrow {I_o}^\prime = \dfrac{{{V_o}}}{{2R}}$………eq. (2)
Comparing equation (1) and (2).
$ \Rightarrow {I_o}^\prime = \dfrac{{{I_o}}}{{\sqrt 2 }}$.

Therefore, the correct option for this problem is option B.

Additional information:
The phase difference is seen when the circuit is having an AC source, the current, resistance and voltage all depend upon the angular frequency of the circuit. The reactance of the inductor is equal to ${{\text{X}}_{\text{L}}} = \omega L$ where $\omega $ is the angular frequency of the circuit and $L$ inductance of the inductor in the circuit. The inductor offers zero resistance in the DC circuit as there the value of the angular frequency is zero. The reactance due to the capacitor in a DC voltage is infinite as the angular frequency is equal to zero.

Note:
The resistance of the elements like inductor or capacitor is known as reactance. Students should always remember the formula of the reactance of the capacitor and inductor. Also, the reactance depends upon the angular frequency of the circuit.