Question

An aeroplane flying horizontally 1 km above the ground is observed at an elevation of ${{60}^{\circ }}$. After 10 s, if its elevation is observed to be ${{30}^{\circ }}$, then find the uniform speed of the aeroplane in km/h?
(a) $\dfrac{240}{\sqrt{2}}$,
(b) $240\sqrt{3}$,
(c) $240$,
(d) None of these.

Answer 1

Hint: We start solving the problem by drawing the given information to get a better view. We then find the total distance travelled by the aeroplane in the given 10 s using the diagram we just drawn. We then find the speed of the aeroplane by dividing the obtained distance with 10 s. We then use the fact that $1s=\dfrac{1}{3600}h$ to get the required value of speed in km/h.

Complete step-by-step answer:
According to the problem, we have an aeroplane flying horizontally 1 km above the ground which is observed at an elevation of ${{60}^{\circ }}$. We need to find the uniform speed of aeroplane in km/h if the angle of elevation is observed to be ${{30}^{\circ }}$ after 10 s.
Let us draw the given information to get a better view.

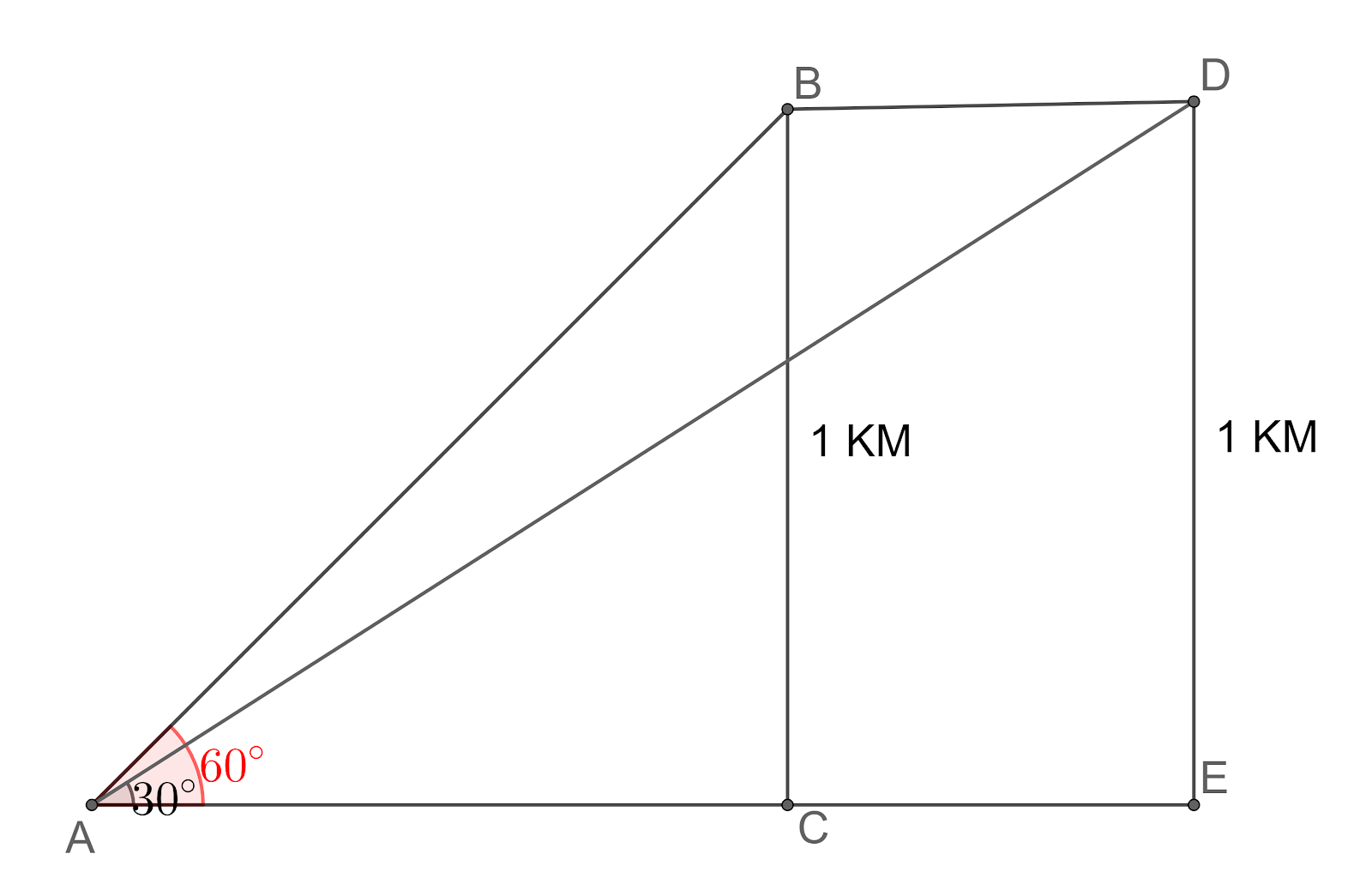
Let us assume that the aeroplane is at point B when the angle of elevation is ${{60}^{\circ }}$ and moves a distance BD after 10 seconds.
Let us first find the distance AC and AD.
From triangle ABC, we get $\tan {{60}^{\circ }}=\dfrac{BC}{AB}$.
$\Rightarrow \sqrt{3}=\dfrac{1}{AB}$.
$\Rightarrow AB=\dfrac{1}{\sqrt{3}}km$ ---(1).
From triangle AED, we get $\tan {{60}^{\circ }}=\dfrac{DE}{AE}$.
$\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{1}{AE}$.
$\Rightarrow AE=\sqrt{3}km$ ---(2).
From the figure we can see that $BE=CD=AE-AB$.
$\Rightarrow BE=\sqrt{3}-\dfrac{1}{\sqrt{3}}$.
$\Rightarrow CD=\dfrac{3-1}{\sqrt{3}}$.
$\Rightarrow CD=\dfrac{2}{\sqrt{3}}km$.
So, the aeroplane travelled $\dfrac{2}{\sqrt{3}}km$ in 10 s. Using we get the speed of the aeroplane as $\dfrac{\dfrac{2}{\sqrt{3}}}{10}=\dfrac{1}{5\sqrt{3}}km/s$.
We know that the 1 hour = 3600 s. Using this we get $1s=\dfrac{1}{3600}h$.
So, we get speed of aeroplane as $s=\dfrac{\dfrac{1}{5\sqrt{3}}}{\dfrac{1}{3600}}km/h$.
$\Rightarrow s=\dfrac{720}{\sqrt{3}}km/h$.
$\Rightarrow s=240\sqrt{3}km/h$.
So, we have found the speed of the aeroplane as $240\sqrt{3}km/h$.

So, the correct answer is “Option (b)”.

Note: We should not stop solving the problem after finding the speed in km/s, as it is mentioned km/h in the problem. Whenever we are asked to solve this type of problems we need to draw the diagram first to get a better view. We have assumed that distance of aeroplane above the ground is not changing throughout the problem. We should not make calculation mistakes while solving this problem.