
An aeroplane flying horizontally at 750m above the ground to an elevation of
Answer
405.6k+ views
Hint: This question is simply related to trigonometric functions. Since the point of observation is the same we will first draw the diagram of the given situation of both the angles so given. Then we will use the trigonometric functions, especially the tan function. Then we will find the exact distance travelled by the plane in 5 seconds. Then we will use the formula of speed to find the speed of aeroplane.
Complete step by step answer:
Given that, An aeroplane flying horizontally at 750m above the ground to an elevation of
Now the diagram can be drawn as,
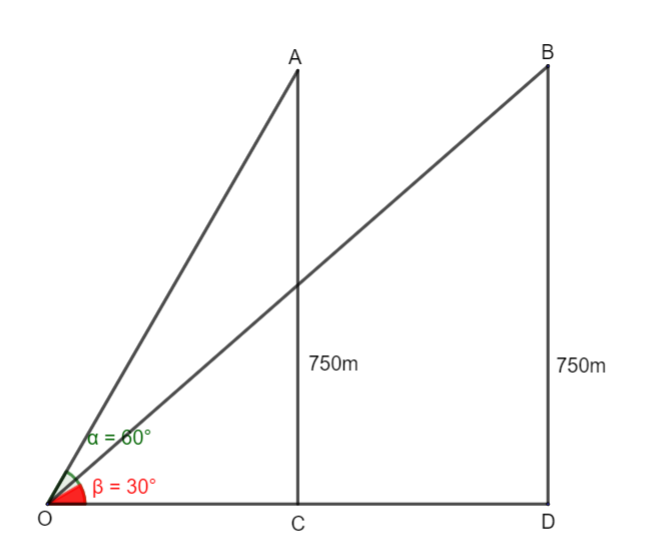
As we can see both the angles now we have to find the distance CD that the airplane has travelled in 5 seconds.
So we will consider the triangles.
In
As we know that
This is the value of OC.
Now in
Now, the distance it travelled in 5 seconds is given by,
Taking 750 common,
This is the distance in meters but we need the distance in km,
Now we have the distance travelled and the time taken to cover the distance so the speed can be given by,
Since time is in seconds we will convert it in hours.
On simplifying we get,
Thus, the speed of the airplane is
Note:
When we solve the problem the most important thing to note is what the situation actually is. Though the elevation is reduced, the height is still the same. This is the biggest mistake students generally make. Second thing to note is we are sometimes asked to find only the distance travelled but here we are about to find the speed also.
For that do observe the units always. Make them in the same measuring system either CGS or MKS or that which is asked to do.
Complete step by step answer:
Given that, An aeroplane flying horizontally at 750m above the ground to an elevation of
Now the diagram can be drawn as,

As we can see both the angles now we have to find the distance CD that the airplane has travelled in 5 seconds.
So we will consider the triangles.
In
As we know that
This is the value of OC.
Now in
Now, the distance it travelled in 5 seconds is given by,
Taking 750 common,
This is the distance in meters but we need the distance in km,
Now we have the distance travelled and the time taken to cover the distance so the speed can be given by,
Since time is in seconds we will convert it in hours.
On simplifying we get,
Thus, the speed of the airplane is
Note:
When we solve the problem the most important thing to note is what the situation actually is. Though the elevation is reduced, the height is still the same. This is the biggest mistake students generally make. Second thing to note is we are sometimes asked to find only the distance travelled but here we are about to find the speed also.
For that do observe the units always. Make them in the same measuring system either CGS or MKS or that which is asked to do.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




