Question

An aeroplane when flying at a height of 3125 m from the ground passes vertically below another plane at an instant when the angle of elevation of the two planes from the same point on the ground are \[{{30}^{\circ }}\] and \[{{60}^{\circ }}\] respectively. Find the distance between the two planes at that instant.

Answer 1

Hint: Use trigonometric values of angles to relate the height at which the aeroplanes are flying and the distance from the point from which aeroplanes are viewed and the base from which height of aeroplane is measured. Use the fact that the base from which the height is viewed is perpendicular to the height of the aeroplane.

Complete step-by-step answer:

We have data regarding two planes flying in the same vertical line at different points. We have to find the height at which one of the planes is flying, given the other one is flying at a height of 3125 m.
Let’s assume that the two planes are viewed from point A on the ground. The plane flying at height of 3125 m is at point D and the other plane is at point C. From point A, plane at C is viewed at an angle of \[{{30}^{\circ }}\] and the plane at D is viewed at an angle of \[{{60}^{\circ }}\]. Let the foot of the line in which planes are flying be at point B, as shown in the figure. We have to calculate the distance between two planes, which is the length of the side CD.

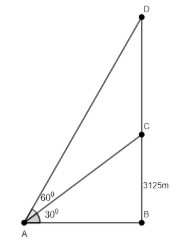
We observe that line AB is perpendicular to the vertical line BD. So, we have \[\vartriangle ABC\] and \[\vartriangle ABD\] as right angled triangles.
In \[\vartriangle ABC\], we have \[\angle BAC={{30}^{\circ }}\]. So, we have \[\tan \left( \angle BAC \right)=\tan \left( {{30}^{\circ }} \right)=\dfrac{1}{\sqrt{3}}\].
We know that tangent of any angle is the ratio of length of perpendicular and base of the triangle.
So, we have \[\tan \left( \angle BAC \right)=\dfrac{BC}{AB}\].
Thus, we have \[\dfrac{BC}{AB}=\dfrac{1}{\sqrt{3}}\].
We can rewrite the above equation as \[AB=\sqrt{3}BC\].
We know that \[BC=3125m\].
Thus, we have \[AB=3125\sqrt{3}m....\left( 1 \right)\].
In \[\vartriangle ABD\], we have \[\angle BAD={{60}^{\circ }}\]. So, we have \[\tan \left( \angle BAD \right)=\tan \left( {{60}^{\circ }} \right)=\sqrt{3}\].
We know that tangent of any angle is the ratio of length of perpendicular and base of the triangle.
So, we have \[\tan \left( \angle BAD \right)=\dfrac{BD}{AB}\].
Thus, we have \[\dfrac{BD}{AB}=\sqrt{3}\].
We can rewrite the above equation as \[BD=\sqrt{3}AB\].
Substituting the value of equation (1) in above equation, we have \[BD=\sqrt{3}\left( 3125\sqrt{3} \right)=9375m\].
We know that \[BD=BC+CD\].
Thus, we have \[9375=3125+CD\].
So, we have \[CD=9375-3125=6250m\].
Hence, the distance between two planes is 6250m.

Note: One must remember the fact that the two planes are in the same vertical line and that line is perpendicular to the base from which the two aeroplanes are viewed. If we don’t consider this fact, we will get an incorrect answer.