Question

An airplane at an altitude of 1 km, flying horizontally at 800 km/hour passes directly over an observer. Find the rate at which it is approaching the observer when it is 1250 meters away from him.

Answer 1

Hint: The rate of change of position of the moving object with respect to the object or the person at rest or in motion will result in the velocity of the moving object. The unit of velocity is derived with respect to time and in SI unit is denoted as meters per second or kilometer per hour.

In this question kilometer per hour has been used as the unit of the speed of the airplane. As the distance between the airplane and the observer is changing continuously with time, so the rate of change of the air-distance of the airplane with the observer will result in the rate at which it is approaching the observer. The use of the Pythagoras theorem has been intensively used here in this question.

Complete step by step answer:
According to the data given in the question, the following path trajectory is followed by the airplane while crossing the observer.

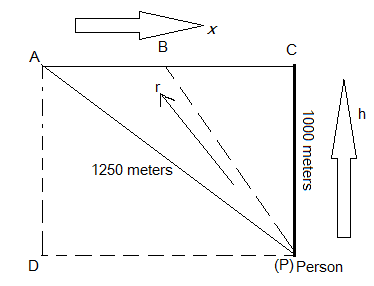
Applying Pythagoras theorem in the right-angled triangle ADP, we get:
$
  A{P^2} = A{D^2} + D{P^2} \\
  {1250^2} = {1000^2} + D{P^2} \\
  D{P^2} = (1250 - 1000)(1250 + 1000) \\
  DP = \sqrt {(250)(2250)} \\
   = \sqrt {562500} \\
   = 750{\text{ meters}} \\
 $

Hence, the horizontal distance between the person at P and the airplane which is 1250 meters away from him is 750 meters.

Now, as the airplane is moving towards the person so, the horizontal distance between the plane and the person as well the air-distance between the person and the plane is changing continuously with time.
So, let us consider the plane is at point B where the horizontal distance between the plane and the person be $x$ and the air-distance between the person and the plane be $r$.

According to the question, applying Pythagoras theorem in triangle BCP, we get: ${r^2} = {x^2} + {h^2}$

Differentiating the equation ${r^2} = {x^2} + {h^2}$ with respect to time $t$ to determine the rate of change of the position of the airplane:

$
  \dfrac{{d\left( {{r^2}} \right)}}{{dt}} = \dfrac{{d\left( {{x^2}} \right)}}{{dt}} + \dfrac{{d\left( {{h^2}} \right)}}{{dt}} \\
  2r\dfrac{{dr}}{{dt}} = 2x\dfrac{{dx}}{{dt}} + 0 \\
  \dfrac{{dr}}{{dt}} = \left( {\dfrac{x}{r}} \right)\dfrac{{dx}}{{dt}} \\
 $

Now, substitute $x = DP = 750;r = 1250{\text{ and, }}\dfrac{{dx}}{{dt}} = 800$ in the equation $\dfrac{{dr}}{{dt}} = \left( {\dfrac{x}{r}} \right)\dfrac{{dx}}{{dt}}$ to determine the value of $\dfrac{{dr}}{{dt}}$ which is the rate at which the airplane is approaching the observer.

$
  \dfrac{{dr}}{{dt}} = \left( {\dfrac{x}{r}} \right)\dfrac{{dx}}{{dt}} \\
   = \left( {\dfrac{{750}}{{1250}}} \right) \times 800 \\
   = 480{\text{ kmph}} \\
 $

Hence, the rate at which it is approaching the observer is 480 kilometers per hour.


Note: It is to be noted down here that the rate of approaching the airplane towards the observer is the air-distance between the airplane and the observer and not the horizontal distance between the airplane and the observer.