
An airplane is flying with a velocity of
Answer
426.9k+ views
Hint:To find the resultant of the given velocity vectors, we can draw a phase diagram of the two velocity vectors as shown below. Since velocity is a vector component, to add two or more vectors we can use the triangle addition of vectors as shown below.
Formula used:
Complete step-by-step solution:
We know that vectors are quantities, which have both direction and magnitude, thus to add two or more vectors, we use the parallelogram law of vector addition. Or we can also use the triangle law of vector addition, which is a simplified version of the parallelogram law of vector addition .
The triangle law of vector addition states the following:
“when two vectors are represented as two sides of the triangle with the order of magnitude and direction, then the third side of the triangle represents the magnitude and direction of the resultant vector”
Consider the diagram as shown below:
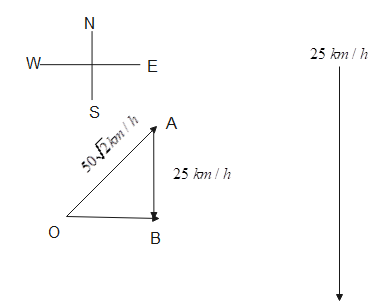
Where,
Then the magnitude of the resultant is given as
Thus,
Note: Using parallelogram law of vector addition, we can also subtract two or more vectors. To account for the negative sign, we can invert the direction of the vector with the negative sign and then add them together. Also note that the vectors can be displaced keeping the direction and the magnitude the same.
Formula used:
Complete step-by-step solution:
We know that vectors are quantities, which have both direction and magnitude, thus to add two or more vectors, we use the parallelogram law of vector addition. Or we can also use the triangle law of vector addition, which is a simplified version of the parallelogram law of vector addition .
The triangle law of vector addition states the following:
“when two vectors are represented as two sides of the triangle with the order of magnitude and direction, then the third side of the triangle represents the magnitude and direction of the resultant vector”
Consider the diagram as shown below:

Where,
Then the magnitude of the resultant is given as
Thus,
Note: Using parallelogram law of vector addition, we can also subtract two or more vectors. To account for the negative sign, we can invert the direction of the vector with the negative sign and then add them together. Also note that the vectors can be displaced keeping the direction and the magnitude the same.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




