
An alloy of gold and copper crystallizes in a cubic lattice in which Au atoms occupy the lattice points at the corner of the cube and Cu atoms occupy the center of each of the cube faces. The formula of the compound is ________.
Answer
444k+ views
Hint: For the atoms present at the corners of the cubic lattice, the number of atoms per unit cell is
Complete answer:
A simple cubic lattice is made up of a large number of cubic unit cells joined together in all directions. A unit cell is the simplest repeating unit of a lattice structure. A diagram of a unit cell of a cubic lattice is given below in which red atoms are placed at its corners and green atoms are occupying center of each face of unit cell:
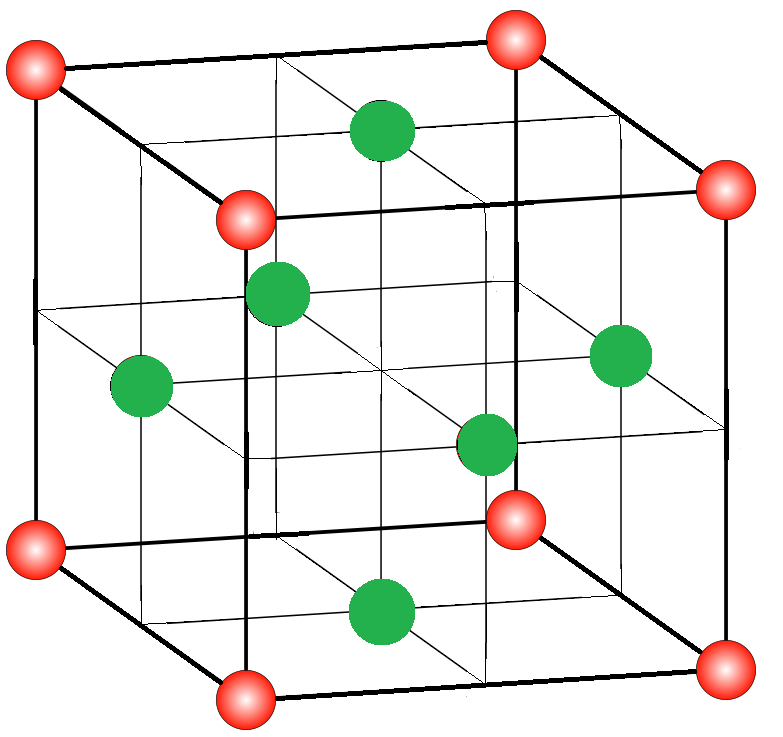
To find the formula of a compound, first, we need to find the number of atoms present in one unit cell.
-The atoms that are present at the corners of a cubic unit cell are shared by a total of eight unit cells, so only one-eighth of the atom will be present in one unit cell. Since there are a total of 8 corners in a cube, so the number of atoms per unit cell will be –
Thus, there will be 1 atom of Au per unit cell.
Now, for the atoms that occupy the center of each face of a cubic unit cell, each such atom is contained by two adjacent unit cells and since there is a total of 6 faces in a cube, so the number of atoms per unit cell will be:
Thus, there will be 3 atoms of Cu per unit cell. So, we have 1 gold atom and 3 copper atoms in a cubic unit cell.
Hence, the formula of the compound is
Note:
There are a total of 7 different types of lattice systems in which few systems have more than one type of unit cells. The total number of these different unit cells is 14 and are known as Bravais lattices.
Complete answer:
A simple cubic lattice is made up of a large number of cubic unit cells joined together in all directions. A unit cell is the simplest repeating unit of a lattice structure. A diagram of a unit cell of a cubic lattice is given below in which red atoms are placed at its corners and green atoms are occupying center of each face of unit cell:

To find the formula of a compound, first, we need to find the number of atoms present in one unit cell.
-The atoms that are present at the corners of a cubic unit cell are shared by a total of eight unit cells, so only one-eighth of the atom will be present in one unit cell. Since there are a total of 8 corners in a cube, so the number of atoms per unit cell will be –
Thus, there will be 1 atom of Au per unit cell.
Now, for the atoms that occupy the center of each face of a cubic unit cell, each such atom is contained by two adjacent unit cells and since there is a total of 6 faces in a cube, so the number of atoms per unit cell will be:
Thus, there will be 3 atoms of Cu per unit cell. So, we have 1 gold atom and 3 copper atoms in a cubic unit cell.
Hence, the formula of the compound is
Note:
There are a total of 7 different types of lattice systems in which few systems have more than one type of unit cells. The total number of these different unit cells is 14 and are known as Bravais lattices.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

The reason why India adopted the policy of nonalignment class 11 social science CBSE

The plastids which are coloured green and colourless class 11 biology CBSE

Earth rotates in which direction A East to west B West class 11 physics CBSE

a Green plastids are called b Plant cell has a big class 11 biology CBSE




