Question

An arch is in the shape of a parabola whose axis is vertically downward and measures $80\,m$ across its bottom ground. Its height is $24\,m$. The measure of the horizontal beam across its cross section at a height of $18\,m$is:
$
  a)\,50 \\
  b)\,40 \\
  c)\,45 \\
  d)\,60 \\
 $

Answer 1

Hint:In this question we will try to make a figure according to the given information and determine the points on parabola at height $18\,m$ where the cross section of beam measures .Then we will write the equation of the parabola. And with the help of equations we will find the answer.

Complete step-by-step answer:

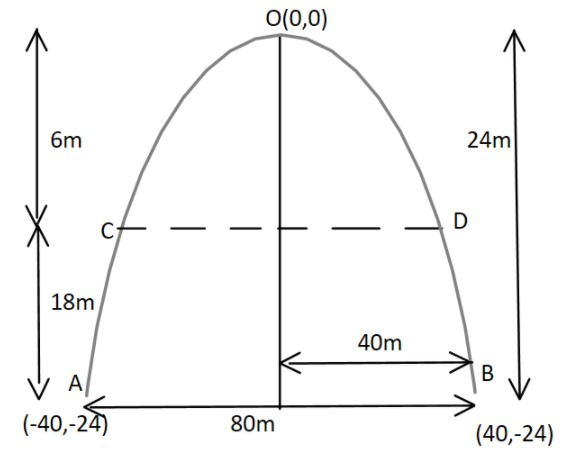
Let equation of the given vertically downward parabola be ${x^2} = - 4ay\,\,\,\,\,\,\,\,\,\,\,\,\, \to (1)$
Given the measure of bottom on ground is $80\,m$
And the highest point is $24\,m$
So we can clearly now find the points A and B‘s coordinates.
$A \equiv ( - 40, - 24)\,\,\,\,\& \,\,\,B \equiv (40, - 24)$
And both of these points lie on parabola so A must satisfy (1)
$
  {(40)^2} = - 4a( - 24) \\
  1600 = 96a \\
  a = \dfrac{{50}}{3}\,\,\,\,\,\,\,\,\,\,\, \to (2) \\
 $
Now putting this value in (1)
$
  {x^2} = - 4\left( {\dfrac{{50}}{3}} \right)y \\
  3{x^2} = - 200y\,\,\,\,\,\,\,\, \to (3) \\
 $
Now we need to find the value of $x$ at $y = - 6$ by putting it in (3)
$
  3{x^2} = - 200( - 6) \\
  3{x^2} = 1200 \\
  {x^2} = 400 \\
  x = \pm 20 \\
 $
Now coordinates of C becomes $( - 20, - 6)$ and D becomes $(20, - 6)$.
Now distance between C and D is,
$
  CD = \sqrt {{{(20 - ( - 20))}^2} + {{( - 6 - ( - 6))}^2}} \\
  CD = \sqrt {{{40}^2} + {0^2}} \\
  CD = 40 \\
 $
So the horizontal beam across its cross section at a height of $18\,m$ is of measure $40\,m$.

So, the correct answer is “Option B”.

Note:The tricky part in the question is that we need to find the measure of height of the horizontal beam across its cross section at a height of $18\,m$. Generally we take $18\,m$ as the ordinate but actually by seeing the figure we can clearly see that $18\,m$ is not ordinate and we need to subtract $24\,m$ from it.