Question

An electrician has to repair an electric fault on a pole of height 5m. She needs to reach a point 1.3m below the top of the pole to undertake the repair work. What should be the length of the ladder that she should use which, when inclined at an angle of ${{60}^{o}}$to the horizontal, would enable her to reach the required position? Also, how far from the foot of the pole should she place the foot of the ladder? (you may take $\sqrt{3}=1.73$).
(a) length of the ladder = 7.4m, distance = 2.14m.
(b) length of the ladder = 4.27m, distance = 3.7m.
(c) length of the ladder = 4.27m, distance = 2.14m.
(d) length of the ladder = 4.7m, distance = 2.14m.

Answer 1

Hint: We start solving the problem by drawing the figure representing all the given information. We find the distance between the foot of the pole and the point where the electrician needs to work. After drawing the given information, we use trigonometric functions to calculate the requires values.

Complete step-by-step solution:
Given that the electrician has to repair an electric pole of height 5m. She needs to reach 1.3m below the top of the pole to undertake the repair work. We need to find the length of the ladder that she uses to climb, when the ladder is inclined at an angle ${{60}^{o}}$to the horizontal.
Let us draw all the given information to get a better view. Let us assume the length of the ladder be y m and the distance between the foot of the pole to the foot of the ladder is x m.

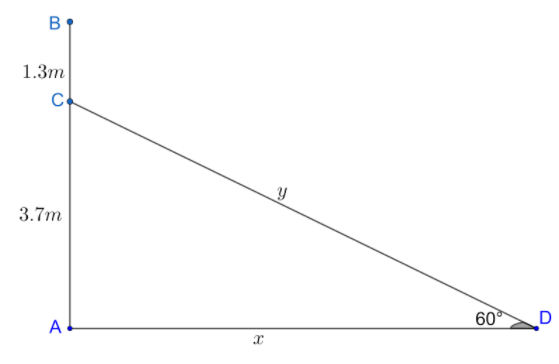
Since the height of the pole is 5m and electrician need to reach a height of 1.3m less than the top point of the pole. So, the electrician needs to reach $\left( 5-1.3 \right)m=3.7m$ from the foot of the pole.
From triangle ADC, we get $\sin \left( {{60}^{o}} \right)=\dfrac{AC}{CD}$.
$\dfrac{\sqrt{3}}{2}=\dfrac{3.7}{y}$.
According to the problem, $\sqrt{3}=1.73$.
$\dfrac{1.73}{2}=\dfrac{3.7}{y}$.
$y=\dfrac{3.7\times 2}{1.73}$.
$y=\dfrac{7.4}{1.73}$.
$y=4.27m$.
$\therefore$ The length of the ladder is $4.27m$.
From triangle ADC, we get $\tan \left( {{60}^{o}} \right)=\dfrac{AC}{AD}$.
$\sqrt{3}=\dfrac{3.7}{x}$.
According to the problem, $\sqrt{3}=1.73$.
$x=\dfrac{3.7}{1.73}$.
$x=2.14m$.
$\therefore$ The distance between the foot of the pole and the foot of the ladder is 2.14m.
$\therefore$ Length of the ladder = 4.27m and distance between the foot of pole and foot of ladder = 2.14m.
The correct option for the given problem is (c).

Note: We should not connect the ladder to the top of the pole as the electrician is not intended to get to the top of the pole. Here in the problem, we took an approximation up to 2-digits in the decimal place. Here ${{60}^{o}}$ is known as angle of elevation and sometimes problems can be asked by using this name. The key point to solve this problem is to set the relation between the unknown sides and the given length of the pole by using the trigonometric ratio for a given elevation angle of ${{60}^{o}}$.