Question

An electron having a charge e moves with a velocity v in X-direction. A magnetic field acts on it in Y-direction. The force on the electron acts in
A. positive direction of Y-axis
B. negative direction of Y-axis
C. positive direction of Z-axis
D. negative direction of Z-axis

Answer 1

Hint:-The concept of Lorentz force must be applied to solve this problem. The Lorentz force is the combined force that a charged particle experiences when it enters a region of electric and magnetic field aligned perpendicular to each other.
Lorentz Force, $L = {F_E} + {F_B}$
where ${F_E}\& {F_B}$ are the forces due to electric field E and magnetic field B, respectively.

Complete step-by-step solution:-
Consider the following region of space with mutually perpendicular electric field, E and magnetic field, B

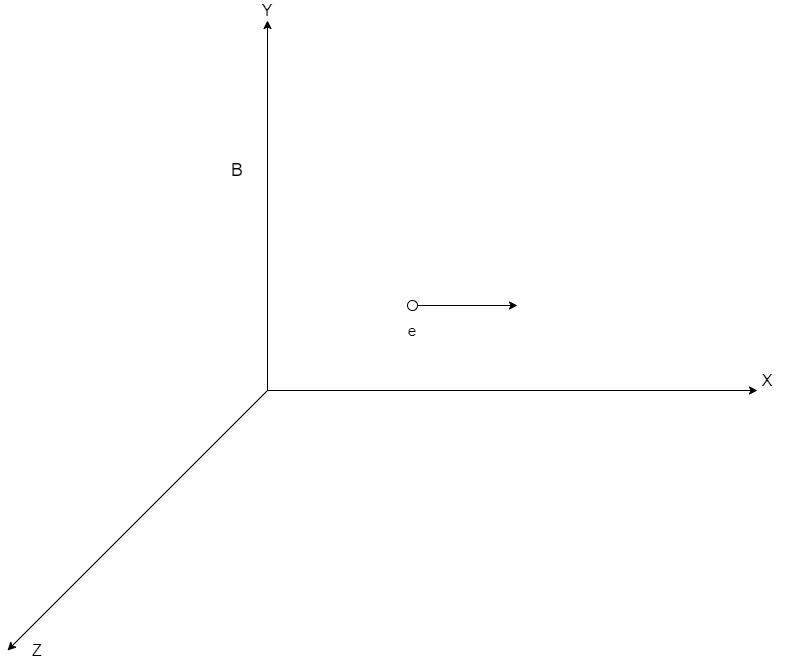
When it enters the above region of space, it experiences combined force due to electric and magnetic fields, known as Lorentz force.
$L = {F_E} + {F_B}$
Since there is no presence of the electric field,
Electric force, ${F_E} = qE = 0$
Magnetic force, ${F_B} = q\left( {\overrightarrow v \times \overrightarrow B } \right)$
where v = velocity and q = charge of the electron, e
We can see that the magnetic force is a cross-product of the velocity and the magnetic field.
The cross-product is a kind of vector product which yields another vector whose direction is perpendicular to the plane containing the two vectors.
In order to determine the direction of the cross-product of two vectors, the right-hand thumb rule should be applied.
In the right hand thumb rule, the 4 fingers should curl in the direction starting from the first vector to the second vector. In doing so, the direction of the thumb represents the direction of the cross-product.

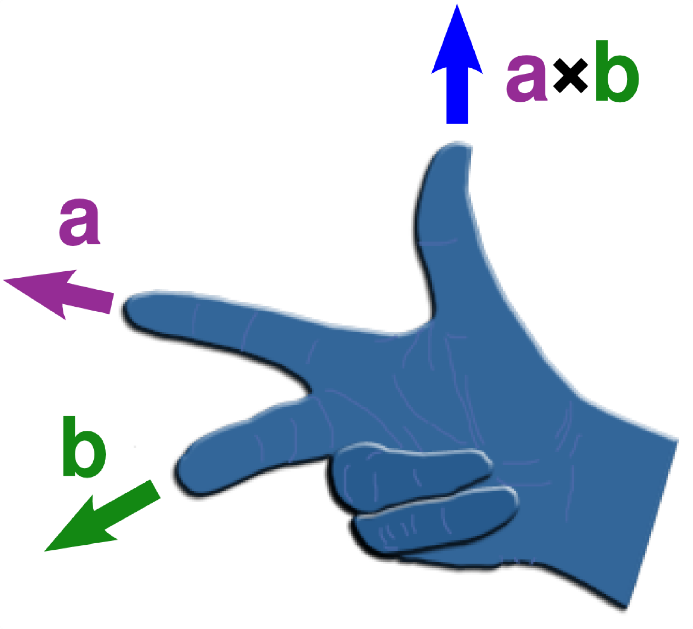
By applying the right-hand thumb rule, we get that the force will be in the positive Z-direction as per the above figure.
Hence, the correct option is Option C.


Note:- There is an alternative method to solve this problem, by using Fleming's left-hand rule.

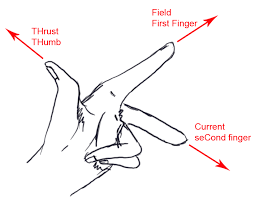
It says that if the left hand is held out as shown in the figure, by orienting the middle finger in the direction of electric field/velocity of the charged particle and the index finger in the direction of the magnetic field, we will be able to observe the direction of force acting on the conductor which is the same as the direction pointed by the thumb.
If we apply Fleming's Left-Hand rule on the above problem, the same answer is obtained.