Question

An equilateral triangle is drawn on the diagonal of a square. The ratio of the area of the triangle to that of the square is:
(a) \[\sqrt{3}:2\]
(b) \[\sqrt{2}:\sqrt{3}\]
(c) \[2:\sqrt{3}\]
(d) \[1:\sqrt{2}\]

Answer 1

Hint: First of all, draw the square with side ‘a’. Now by using Pythagoras Theorem, find the length of the diagonal which would be the side of the equilateral triangle. Now, find the ratio of the area of the triangle to the square by using the formula for the equilateral triangle as\[\dfrac{\sqrt{3}}{4}{{\left( Side\text{ }of\text{ }the\text{ }equilateral\text{ }triangle \right)}^{2}}\] and square as \[{{\left( side\text{ }of\text{ }square \right)}^{2}}\]

Complete step-by-step answer:
We are given that an equilateral triangle is drawn on the diagonal of the square. We have to find the ratio of the area of the triangle to that of the square. Let us first draw an equilateral triangle on the diagonal of the square of side ‘a’.

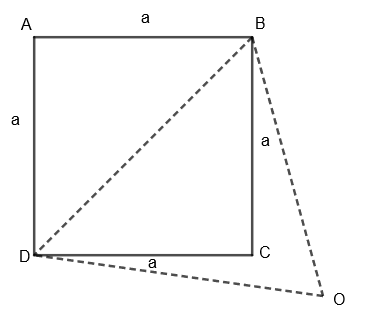
Now, let us consider the square and equilateral triangle individually. Let us consider a square of side length ‘a’.

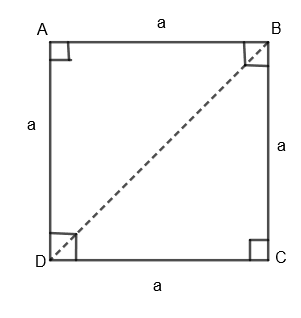
Here, ABCD is our equilateral triangle with each side length equal to ‘a’. We know that in the square, every side is equal and perpendicular to the adjacent sides. So, we get \[\Delta BCD\] as the right-angled triangle, where C is the right angle. We know that, for a right-angled triangle, according to Pythagoras Theorem,
\[{{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}={{\left( Hypotenuse \right)}^{2}}\]
So, by applying Pythagoras theorem in \[\Delta BCD\], we get
\[{{\left( BC \right)}^{2}}+{{\left( CD \right)}^{2}}={{\left( BD \right)}^{2}}\]
By substituting the values of BC = a and CD = a, we get,
\[{{a}^{2}}+{{a}^{2}}={{\left( BD \right)}^{2}}\]
\[\Rightarrow {{\left( BD \right)}^{2}}=2{{a}^{2}}\]
By taking square root on both the sides of the above equation, we get,
\[BD=a\sqrt{2}\]
So, we get the length of BD which is diagonal of the square as \[a\sqrt{2}\]. Now, we are given that the equilateral triangle is drawn on the diagonal of the square, so we get each side of the equilateral triangle = diagonal of the square = \[a\sqrt{2}\].

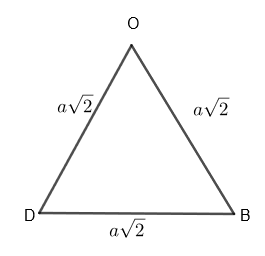
We know that, area of the equilateral triangle \[=\dfrac{\sqrt{3}}{4}{{\left( length\text{ }of\text{ }the\text{ }side\text{ }of\text{ }the\text{ }triangle \right)}^{2}}\]
By substituting the length of the side of the triangle = \[a\sqrt{2}\], we get,
Area of \[\Delta OBD=\dfrac{\sqrt{3}}{4}{{\left( a\sqrt{2} \right)}^{2}}=\dfrac{\sqrt{3}.{{a}^{2}}.2}{4}=\dfrac{\sqrt{3}{{a}^{2}}}{2}\]
Also, we know that the area of the square of the triangle = \[{{\left( length\text{ }of\text{ }the\text{ }side\text{ }of\text{ }the\text{ }triangle \right)}^{2}}\].
By substituting the length of the side of the square = a, we get,
Area of the square ABCD \[={{\left( a \right)}^{2}}\].
So, we get the ratio of the area of the triangle to that of the square as,
\[\dfrac{\text{Area of }\Delta \text{OBD}}{\text{Area of }\square \text{ABCD}}=\dfrac{\dfrac{\sqrt{3}{{a}^{2}}}{2}}{{{a}^{2}}}\]
By canceling the like terms from RHS, we get,
\[\dfrac{\text{Area of }\Delta \text{OBD}}{\text{Area of }\square \text{ABCD}}=\dfrac{\sqrt{3}}{2}\]
Hence, option (a) is the right answer.

Note: In this question, some students get confused as to why we have taken BD as the diagonal of the square and not AC. So, they must note that the square is one of the most symmetrical polygons we have and the length of both the diagonals of the square is equal. So, it would not make the difference whether we take diagonal BD or diagonal AC because the length would be \[a\sqrt{2}\] only which is going to be used to make the equilateral triangle. Also, take care while taking the sides of the square and triangle which are different while calculating the area.