
An equilateral triangle of side
Answer
505.2k+ views
Hint: First use the property of the equilateral triangle after constructing an altitude from the vertex D on the side BC. After that use the property of the subtended angle by an arc to get the desired result.
Complete step by step solution:
We have given an equilateral triangle of side
The goal is to find the radius of the circle.
Now, draw a figure in which an equilateral triangle of side
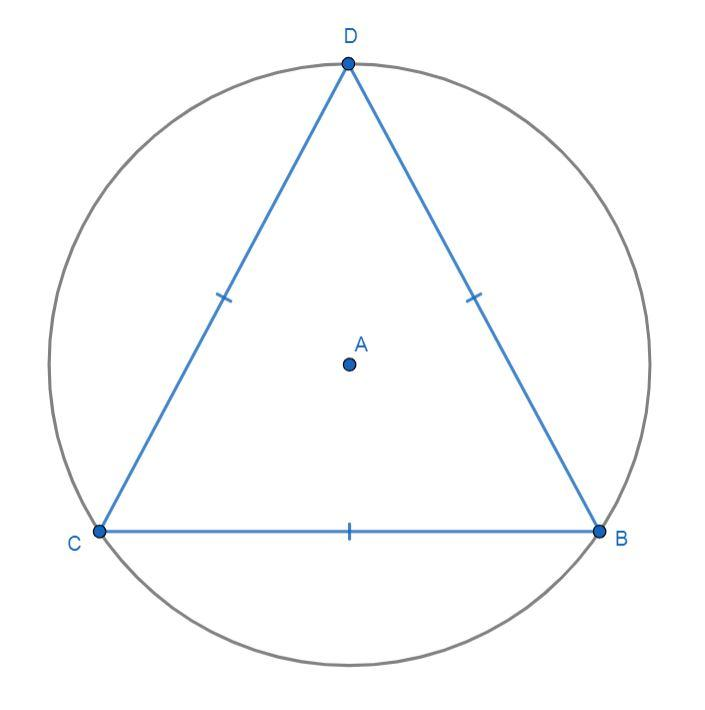
In the above figure,
Since ABC is an equilateral triangle, then the altitude from its vertex to the corresponding side is the perpendicular bisector of the side even if it passes through the circumcenter of the triangle.
Now, for starting the problem we have made some construction. So, draw an altitude from the vertex
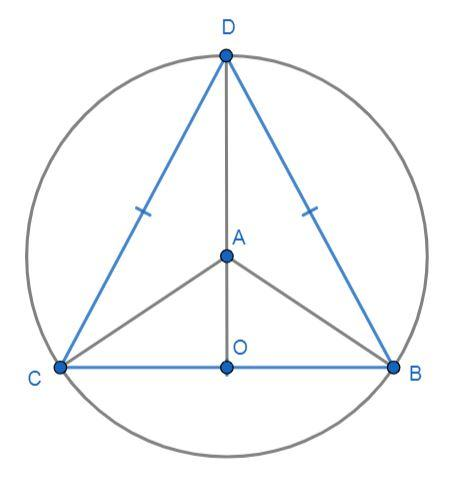
Now, take a look on the triangles
Therefore, using the
Then we have,
We know that the angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle. Then we can write,
As
Using it we have,
Now, we can easily, break the angle
As we have
Substitute the value
As the altitude from the vertex D on the side, bisect the side BC, then
Substitute the length of a side,
Now, in the triangle CAO, we have
Now, apply the trigonometric ratio in the triangle CAO, we have
Substitute the values:
Solve the equation for
Therefore, the radius of the circle is
Note: The altitude drawn from the vertex on the side is perpendicular to the side and bisect it and also the altitude passes through the circumcenter of the triangle.
Complete step by step solution:
We have given an equilateral triangle of side
The goal is to find the radius of the circle.
Now, draw a figure in which an equilateral triangle of side

In the above figure,
Since ABC is an equilateral triangle, then the altitude from its vertex to the corresponding side is the perpendicular bisector of the side even if it passes through the circumcenter of the triangle.
Now, for starting the problem we have made some construction. So, draw an altitude from the vertex

Now, take a look on the triangles
Therefore, using the
Then we have,
We know that the angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle. Then we can write,
As
Using it we have,
Now, we can easily, break the angle
As we have
Substitute the value
As the altitude from the vertex D on the side, bisect the side BC, then
Substitute the length of a side,
Now, in the triangle CAO, we have
Now, apply the trigonometric ratio in the triangle CAO, we have
Substitute the values:
Solve the equation for
Therefore, the radius of the circle is
Note: The altitude drawn from the vertex on the side is perpendicular to the side and bisect it and also the altitude passes through the circumcenter of the triangle.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




