Question

An Explosion breaks a rock into three posts in a horizontal plane. Two of them go off at right angles to each other. The first part of mass 1 kg moves with a speed of 12 m/s and the second part of mass 2 kg moves with 8 m/s speed. If the third part flies off with 4 cm/s speed, then it's mass is
A. 3kg
B. 5kg
C. 7kg
D. 17kg

Answer 1

Hint: In this type of question as we know initial rock is at rest and after explosion it breaks into three parts. So at this place we apply the conservation of linear momentum.
Conservation of linear momentum states that initial momentum of the object remains the same after collision.

Complete step-by-step answer:
The given explosion breaks a rock into three parts.

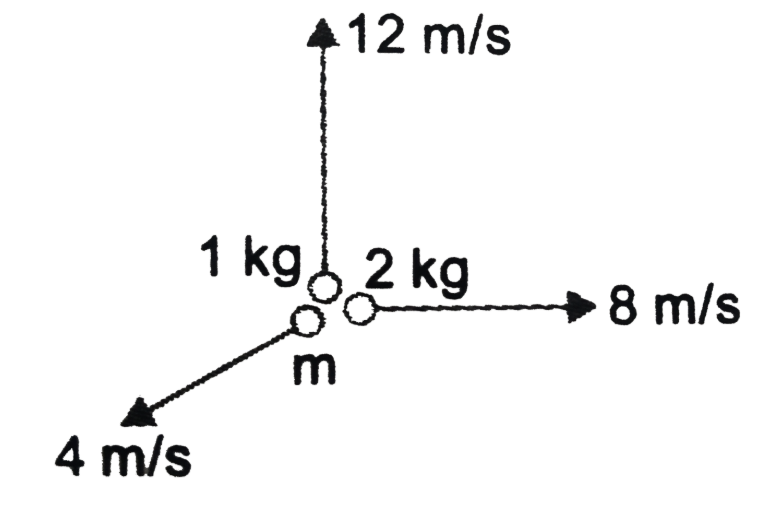
As given two parts of mass \[{{m}_{1}}=1\text{ kg}\] and mass \[{{m}_{2}}=2\text{ kg}\] moves perpendicular with speed \[{{v}_{1}}=12\text{ m/s}\] and \[{{\text{v}}_{2}}=8\text{ m/s}\] respectively.
Linear momentum of first part \[\left( {{p}_{1}} \right)=mass\times speed\]
\[={{m}_{1}}{{v}_{1}}\]
\[\Rightarrow {{p}_{1}}=1\times 12=12\text{ kg m/s}\]
Linear momentum of second part \[\left( {{p}_{2}} \right)=mass\times speed\]
\[={{m}_{2}}\times {{v}_{2}}\]
\[\Rightarrow {{p}_{2}}=2\times 8=16\text{ kg m/s}\]
\[{{P}_{resultant}}=\sqrt{{{p}_{1}}^{2}+{{p}_{2}}^{2}+2{{p}_{1}}{{p}_{2}}\cos \theta }\]
\[\theta =\] Angle Between the momentum of Both Parts.
\[{{P}_{resultant}}=\sqrt{{{\left( 12 \right)}^{2}}+{{\left( 16 \right)}^{2}}+2\times 12\times 16\cos 90{}^\circ }\]
\[=\sqrt{144+256}=\sqrt{400}=20\text{ kg m/s }..........\text{ 1}\].
Linear momentum of third part \[\left( {{p}_{3}} \right)=mass\times speed\]
\[={{m}_{3}}\times {{v}_{3}}\]
\[=4\text{ }{{\text{m}}_{3}}\text{ }......\text{ 2}\]
Initial Momentum of rock \[=mass\times speed\]
\[=m\times 0\]
\[=0\text{ kg m/s}\]
By momentum conservation
Initial momentum = Final momentum
\[\Rightarrow 0={{p}_{1}}+{{p}_{2}}+{{p}_{3}}\]
\[\Rightarrow {{p}_{3}}=-\left( {{p}_{1}}+{{p}_{2}} \right)\text{ }.........\text{ 3}\]
Negative sign shows the third part of rock move in the opposite direction as a result of part First and second.
Substitute the value of \[{{p}_{3}}\] and \[{{p}_{resul\tan t}}\] from equation 1 and 2 equation 3
\[\Rightarrow 4{{m}_{3}}=20\]
\[\Rightarrow {{m}_{3}}=\dfrac{20}{4}=5\text{ kg}\]
Therefore, the correct choice is (B) 5 kg

Note: As we know the initial rock is at rest so the initial momentum will be zero. This initial momentum is equal to the final momentum of each part. It is possible due to conservation of momentum.