Question

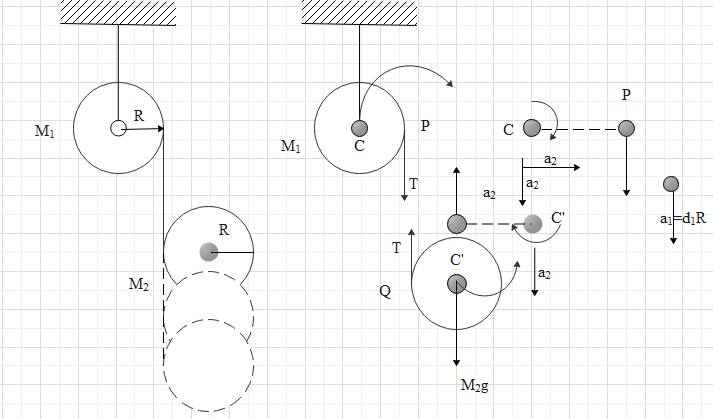
An extensible string is wound over a rough pulley of mass ${M_1}$ and radius $R$ and a cylinder of mass ${M_2}$ and radius $R$ such that as the cylinders roll down, the string unwound over the pulley as well the cylinder. Find the acceleration of cylinder ${M_2}$.

Answer 1

Hint: From the given information we can find that the pulley has only rotational motion but the cylinder will have both rotational and translational motion.
Torque is a product of the moment of inertia and angular acceleration.
$\tau = I\alpha $
Where $I$ is the moment of inertia and $\alpha $ is the angular acceleration.
Torque can also be found out by multiplying the force with the perpendicular distance.
$\tau = F \times R$.
Here the force acting is the tension $T$ in the string and the perpendicular distance is $R$
Using the above two-equation, we can find the angular acceleration of both pulley and cylinder.
The linear acceleration of the cylinder can be found by writing the equation of motion for the cylinder.
The acceleration of the point P and Q will be the same since both are connected with the same string.
Using all this information, we can write equations and solve them for finding the acceleration of ${M_2}$.

Complete step by step answer:
Given the mass of the pulley is ${M_1}$
The radius of the pulley is $R$.
The mass of the cylinder is ${M_2}$.
The radius of the cylinder is $R$.
Now the pulley has only angular acceleration let this be denoted as ${\alpha _1}$
This cylinder has both angular acceleration and linear acceleration.
Let the linear acceleration of the cylinder be denoted as ${a_2}$ and the angular acceleration be denoted as ${\alpha _2}$.
Now let us derive the equation for angular acceleration for the pulley
Let the torque acting on the pulley be $\tau $.
We know that torque is a product of moment of inertia and angular acceleration.
$\tau = I\alpha $
Since pulley is disc shaped the moment of inertia of the pulley is
${I_1} = \dfrac{1}{2}{M_1}{R^2}$
Therefore,
$\tau = \dfrac{1}{2}{M_1}{R^2} \times {\alpha _1}$ ……………………..(1)
Torque can also be found out by multiplying the force with the perpendicular distance.
$\tau = F \times R$ …………………………………………….(2)
Here the force acting is the tension $T$ in the string and the perpendicular distance is $R$
On substituting we get
$\tau = T \times R$ ………………………………………………..(3)
Now let us equate equations 1 and 3
$\dfrac{1}{2}M_1R^2 \times \alpha _1 = T \times R$
$\Rightarrow {\alpha _1} = \dfrac{{2T}}{{{M_1}R}} $

This is the angular acceleration in the pulley.
Now let us find the angular acceleration in the cylinder. Moment of inertia of the cylinder is
${I_2} = \dfrac{1}{2}{M_2}{R^2}$
The torque can be written as
$\tau = {I_2}{\alpha _2}$
$\tau = \dfrac{1}{2}{M_2}{R^2} \times {\alpha _2}$ ………………………...(4)
The force acting here is tension. And perpendicular distance is $R$
Therefore, using equation 3
$\tau = T \times R$ …………………….(5)
Equating equations 4 and 5
$\dfrac{1}{2}M_2R^2 \times \alpha _2 = T \times R$
$ \Rightarrow {\alpha _2} = \dfrac{{2T}}{{{M_2}R}} $
This is the angular acceleration of the cylinder.
In order to find the linear acceleration of the cylinder let us write the equation of motion for this cylinder.
The net force acting on the cylinder will be mass times acceleration
$F = M_2a_2$
The forces acting on the cylinder are force due to gravity ${M_2}g$ and tension $T$.
Therefor net force can be written as
$M_2a_2= M_2g - T$
$ \Rightarrow T = M_2(g - {a_2})$ …………………………………..(6)
Let us denote of the acceleration at point P as ${a_p}$
Acceleration will be the product of angular acceleration and the perpendicular distance.
$a = \alpha \times R$
Therefore
At P, $a_P = \alpha _1R$
Let the acceleration of point Q be ${a_Q}$
This will be the net acceleration due to translation and rotation.
Thus,
${a_Q} = {a_2} - {\alpha _2}R$
The acceleration of the point P and Q will be the same since both are connected with the same string.
Thus
${a_P} = {a_Q}$
That is,
$\alpha _1 R = a_2 - \alpha _2R $
$\Rightarrow a_2 = \alpha _1R + \alpha _2R $
Substitute the value of ${\alpha _1}$ and ${\alpha _2}$ in this equation.
$a_2 = \dfrac{2T}{M_1R}R + \dfrac{2T}{M_2R}R$
$\Rightarrow a_2 = \dfrac{2T\left(M_1 + M_2 \right)}{M_1M_2} $
Substitute the value of tension from equation 6
$a_2 = \dfrac{2M_2(g - a_2)\left(M_1 + M_2 \right)}{M_1M_2}$
$\Rightarrow a_2 = \dfrac{{2g\left(M_1+M_2 \right)}}{{{M_1}}} - \dfrac{2a_2\left(M_1+M_2 \right)}{M_1} $
$\Rightarrow M_1a_2 = 2g\left( M_1 +M_2 \right) - 2a_2\left( {{M_1} + {M_2}} \right) $

$\therefore a_2 = \dfrac{2g\left(M_1 + M_2 \right)}{3M_1 + 2M_2} $. This is the acceleration of cylinder ${M_2}$.

Note:
Hear the pulley has only rotational motion. But the cylinder has both rotational and translational motion. The cylinder is moving downwards with rotation. Whereas the pulley is rotating at the given place itself it does not have a translational motion.
The points P and Q will have the same acceleration because they are connected by the same string. That is why we were able to equate the values of the net acceleration of P and Q.