Question

An ideal gas follows a process, PT=constant. The correct graph between pressure and volume is:
(A)

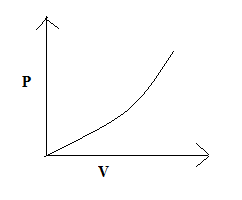
(B)

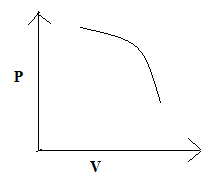
(C)

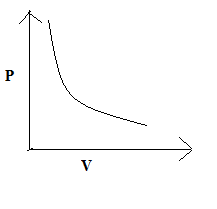
(D)

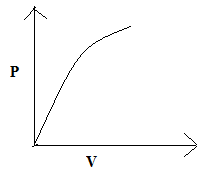
Answer 1

Hint: To solve this question we first need to look into Boyle’s law and Charles’ law. According to Boyle’s law, the volume of a given mass of a gas is inversely proportional to its pressure. According to Charles' law, for a fixed mass of an ideal at a constant pressure, its volume is directly proportional to the temperature. Then, we will use the information provided in the question and substitute it into the ideal gas equation in order to establish a relationship between pressure and volume.

Complete step by step answer:
Before solving this question, first let us look into some of the gas laws:
Boyle’s law: According to Boyle’s law, the volume of a given mass of a gas is inversely proportional to its pressure. That is:
$ V\propto \cfrac { 1 }{ P } $
Where V is the volume of the gas and P is the pressure exerted by the gas. Therefore:
$ V=k\times \cfrac { 1 }{ P } $
Where k is the proportionality constant. Hence,
$ PV=k$
This means the product of the pressure and volume for a given amount of a gas is a constant at constant temperature.
Boyle’s law proves that gases are compressible. If we increase the pressure, the gases will become denser. Hence we can say that at a constant temperature, the density of a gas is directly proportional to its pressure for a fixed mass of a gas.
So, if m is the mass of a gas, V is its volume and P is its pressure, then its density d will be:
$ d=\cfrac { m }{ V } $
Now, according to Boyle’s law, $ PV=k$ or $ V=k\times \cfrac { 1 }{ P } $
Putting this value of V in the density formula,
$d=\cfrac { m }{ \cfrac { k }{ P } } $
$\Rightarrow d=\cfrac { m }{ k } \times P={ k }^{ \prime }P$
Where ${ k }^{ \prime }=\cfrac { m }{ k }$, another constant.

Therefore at higher altitudes the air is less dense since at higher altitudes the pressure is very low. This results in altitude sickness.
Now if we look at the ideal gas equation which states that the product of the volume and pressure of a gas is equal to the product of its number of moles, the temperature and the gas constant:
PV=nRT
If we taking a fixed amount of a gas at constant temperature, this will imply that:
PV=k
Where k=nRT, a constant
This is actually Boyle's law.

Charles’ law: It states that for a fixed mass of an ideal at a constant pressure its volume will be directly proportional to the temperature.
$ V\propto T$
$ \Rightarrow V=kT$ where k is the constant of proportionality.
Now, let us solve the question:
In the question it is given that PT=constant=k (let’s say)
$ \Rightarrow T=\cfrac { k }{ P } $....(1)
Now using the ideal gas equation:
PV=nRT
$\Rightarrow P=\cfrac { nRT }{ V } $
Substituting equation (1) in the above equation:
$ \Rightarrow P=\cfrac { nRk }{ PV } $
$ \Rightarrow { P }^{ 2 }\propto \cfrac { I }{ V } $
So, the correct answer is “Option C”.

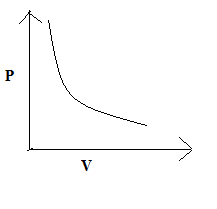
Note: The P versus V graph in accordance with Boyle’s law will also look like (C) since according to Boyle’s law the pressure and volume for a fixed mass of a gas are inversely proportional to each other provided the temperature is kept constant.