
An inclined plane is inclined at an angle
A.
B.
C.
D.
Answer
492.6k+ views
Hint: Draw the free body diagram of the given question by assuming the inclined plane as a triangle with the angle of
Step by Step Solution:
When a body is inclined with a plane at an angle of
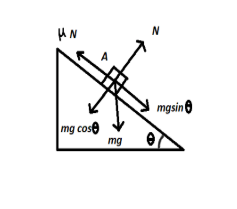
In the above given figure,
Now, the force acting due to the body of mass
Now, from the figure A, we can see that
Therefore, in order to make the body just most up the inclined plane, a force greater than
Therefore,
Where
We know that
Therefore,
So, the net force along the inclined plane is
Therefore,
The minimum force required to move the body just up the inclined plane is
Or option C.
Note: The minimum force required to push the body up the incline plane. It must be equal to the net maximum force acting along the plane of incline. The friction for which the body does not move is called the static friction. The friction for which the body moves is called the kinetic friction. The minimum force required will be equal to maximum value of friction.
Step by Step Solution:
When a body is inclined with a plane at an angle of

In the above given figure,
Now, the force acting due to the body of mass
Now, from the figure A, we can see that
Therefore, in order to make the body just most up the inclined plane, a force greater than
Therefore,
Where
We know that
Therefore,
So, the net force along the inclined plane is
Therefore,
The minimum force required to move the body just up the inclined plane is
Or option C.
Note: The minimum force required to push the body up the incline plane. It must be equal to the net maximum force acting along the plane of incline. The friction for which the body does not move is called the static friction. The friction for which the body moves is called the kinetic friction. The minimum force required will be equal to maximum value of friction.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




