
Answer
462k+ views
Hint: We will draw a free body diagram showing both the forces and then according to the angle of the rope we will find the relation between the two forces, i.e. the force of gravity and the horizontal force on the stone.
Formula used:
Force on an object of mass m due to gravity of earth
${{F}_{g}}=mg$
Complete answer:
First, we will draw the free body diagram. As the support is given to be rigid, we will assume that the rope does not break, and its end remains fixed on the support. We will also assume that the rope remains taut throughout. The tension in the string can be ignored as it balances the two forces and is not required to solve this problem
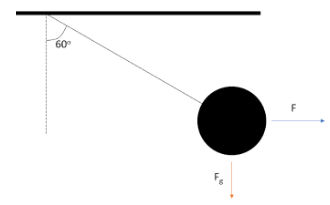
Now as we can see the ratio of the two forces, the external force and the force due to gravity will be given by
$\dfrac{F}{{{F}_{g}}}=\tan {{60}^{o}}=\sqrt{3}$
The force due to gravity will be equal to ${{F}_{g}}=mg=100\times 9.8=980N$.
When we put in this value of the force due to gravity, we will get the horizontal force required to displace it through an angle ${{60}^{o}}$ from the mean position as
\[\dfrac{F}{{{F}_{g}}}=\sqrt{3}\Rightarrow F=\sqrt{3}{{F}_{g}}=980\sqrt{3}N\]
So, the correct answer is “Option B”.
Note:
Take care that the tension on string will be the opposite of resultant of the two forces acting on the ball and will keep it in rest. This force is ignored here for this problem. The value of g must be chosen according to the value given in question or looking at the options. Here we can see that the options are such that the value of 9.8 $m{{s}^{-2}}$ must be taken.
Formula used:
Force on an object of mass m due to gravity of earth
${{F}_{g}}=mg$
Complete answer:
First, we will draw the free body diagram. As the support is given to be rigid, we will assume that the rope does not break, and its end remains fixed on the support. We will also assume that the rope remains taut throughout. The tension in the string can be ignored as it balances the two forces and is not required to solve this problem

Now as we can see the ratio of the two forces, the external force and the force due to gravity will be given by
$\dfrac{F}{{{F}_{g}}}=\tan {{60}^{o}}=\sqrt{3}$
The force due to gravity will be equal to ${{F}_{g}}=mg=100\times 9.8=980N$.
When we put in this value of the force due to gravity, we will get the horizontal force required to displace it through an angle ${{60}^{o}}$ from the mean position as
\[\dfrac{F}{{{F}_{g}}}=\sqrt{3}\Rightarrow F=\sqrt{3}{{F}_{g}}=980\sqrt{3}N\]
So, the correct answer is “Option B”.
Note:
Take care that the tension on string will be the opposite of resultant of the two forces acting on the ball and will keep it in rest. This force is ignored here for this problem. The value of g must be chosen according to the value given in question or looking at the options. Here we can see that the options are such that the value of 9.8 $m{{s}^{-2}}$ must be taken.



