
An isolated conductor of any shape has a net charge of $ + 15\mu C$. Inside the conductor is a cavity within which is a point-charge of $ + 3.0\mu C$. What is the charge on the cavity wall and on the outer surface of the conductor?
Answer
520.9k+ views
Hint: Here we first know that the net electric field inside any conductor is always zero there for net charge inside the conductor is also zero. To achieve this $ - 3.0\mu C$ must develop on the cavity so we get $ + 3.0\mu C - 3.0\mu C = 0\mu C$ and also keeping in mind the charge neutrality a $ + 3.0\mu C$ will get developed on the outer surface of the conductor resulting in $ + 15\mu C + 3.0\mu C = + 18\mu C$ inside the conductor.
Complete Step-by-Step solution:
We know that the charges on the conductor reside on the conductor surface, that is the charge $ + 15\mu C$ is present on the surface of the conductor. A point charge is present in a cavity inside the conductor as can be seen from the figure 1.
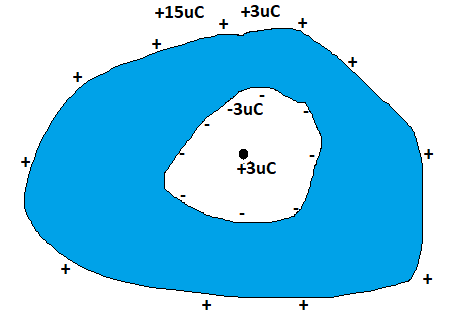
Now we know that the Gaussian surface is an imaginary surface that we use to calculate the flux of a vector electric field. In this question, the Gaussian surface is that surface where the electric field lines are normal to the surface. Here the Gaussian surface is chosen such that it is inside the conductor and enclosing the cavity.
And we know that the net electric field inside any conductor is always zero. So the net charge enclosed inside the Gaussian surface is also zero.
For this to happen a charge equal to $ - 3.0\mu C$must develop on the cavity that is
$ + 3.0\mu C - 3.0\mu C = 0\mu C$
Similarly, now a charge of $ + 3.0\mu C$ will get developed on the outer surface of the conductor where $ + 15\mu C$ charge is already present so the total charge on the outer surface of the conductor is
$ + 15\mu C + 3.0\mu C = + 18\mu C$
Hence a charge of $ - 3.0\mu C$ is on the cavity wall and a charge of $ + 18\mu C$ on the outer surface of the conductor.
Note: For these types of questions, we need to know the basics of Gaussian law and the properties of charges and electric fields. We need to remember that the electric field inside a conductor is always zero and charge neutrality conditions always hold, that is when a negative charge is developed in one side of the conductor an equal and opposite charge form on the other side of the conductor.
Complete Step-by-Step solution:
We know that the charges on the conductor reside on the conductor surface, that is the charge $ + 15\mu C$ is present on the surface of the conductor. A point charge is present in a cavity inside the conductor as can be seen from the figure 1.

Figure 1
Now we know that the Gaussian surface is an imaginary surface that we use to calculate the flux of a vector electric field. In this question, the Gaussian surface is that surface where the electric field lines are normal to the surface. Here the Gaussian surface is chosen such that it is inside the conductor and enclosing the cavity.
And we know that the net electric field inside any conductor is always zero. So the net charge enclosed inside the Gaussian surface is also zero.
For this to happen a charge equal to $ - 3.0\mu C$must develop on the cavity that is
$ + 3.0\mu C - 3.0\mu C = 0\mu C$
Similarly, now a charge of $ + 3.0\mu C$ will get developed on the outer surface of the conductor where $ + 15\mu C$ charge is already present so the total charge on the outer surface of the conductor is
$ + 15\mu C + 3.0\mu C = + 18\mu C$
Hence a charge of $ - 3.0\mu C$ is on the cavity wall and a charge of $ + 18\mu C$ on the outer surface of the conductor.
Note: For these types of questions, we need to know the basics of Gaussian law and the properties of charges and electric fields. We need to remember that the electric field inside a conductor is always zero and charge neutrality conditions always hold, that is when a negative charge is developed in one side of the conductor an equal and opposite charge form on the other side of the conductor.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




