Question

An object is placed at a distance of $10cm$from a convex mirror of focal length$15cm$. Find the position and the nature of the image formed.

Answer 1

Hint: For a convex mirror, the focal length as well as image distance, both are taken as positive. Convex mirror always forms a virtual and erect image. We will use a mirror formula to calculate the image distance and magnification formula to calculate the nature of the image formed.
Formula used:
Mirror formula, $\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}$
Magnification, $m=\dfrac{-v}{u}$
Complete step by step answer:
A convex mirror is a type of curved mirror in which the reflective surface bulges toward the light source. Convex mirror is also called a diverging mirror because it reflects the light outwards and is therefore not used to focus light.
Convex mirrors always form a virtual image because the focus and the centre of curvature are imaginary points inside the mirror and cannot be reached. This means that the images formed by a convex mirror cannot be projected onto a screen as real images. Also, the image formed is smaller than the object projected, but gets larger as the object approaches the convex mirror.

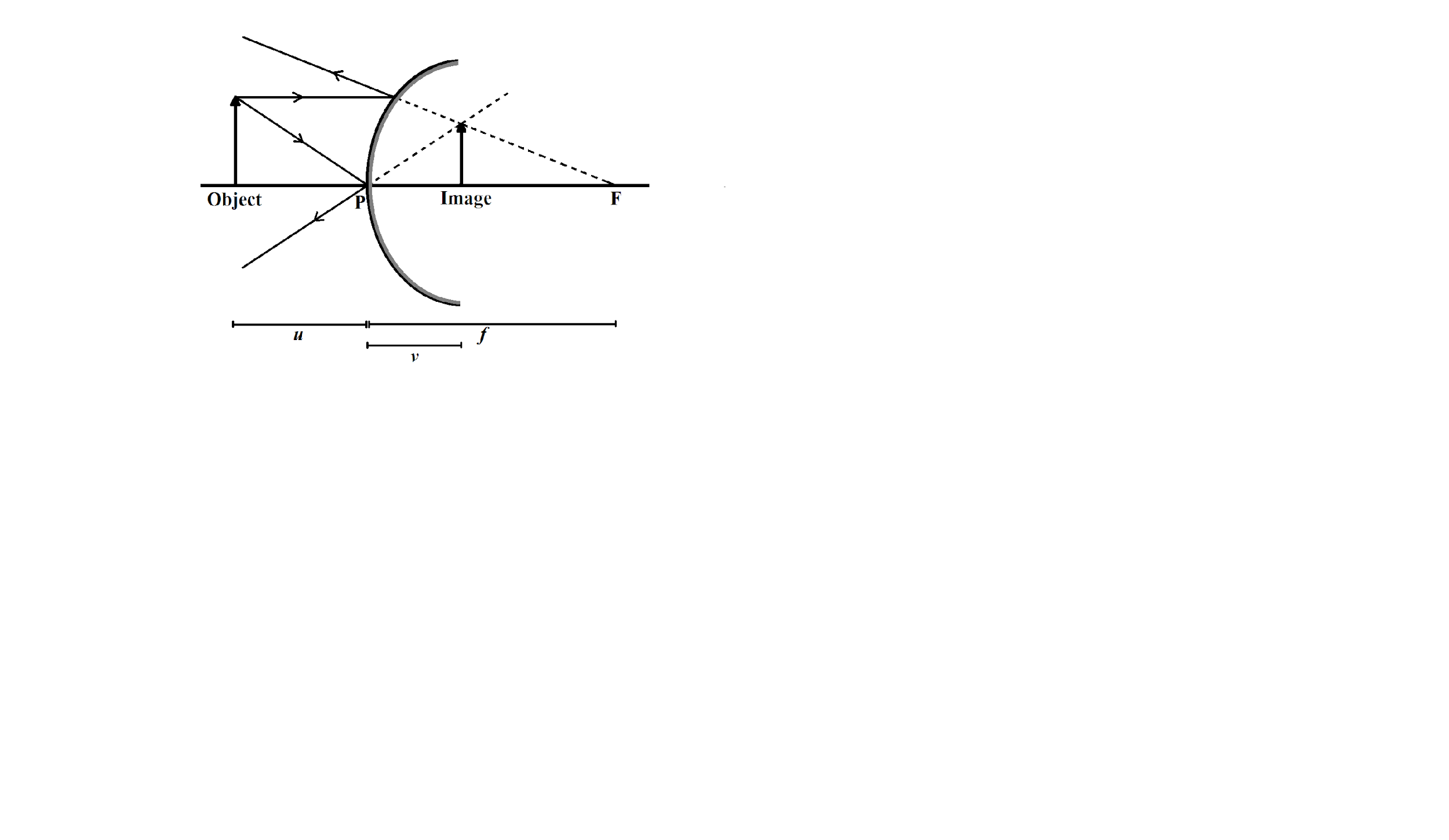
We are given that an object is placed at a distance of $10cm$from a convex mirror of focal length$15cm$
Object distance,$u=-10cm$
Focal length, $f=15cm$
We have to calculate the position and nature of the image formed
Image distance is considered as$v$
Using Mirror formula,
$\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}$
Where,
$v$is the image distance
$u$is the object distance
$f$is the focal length of mirror
In the Mirror formula, object distance is already considered as negative. We have to put the magnitude only in the formula while doing calculations.
Putting values,
 $u=\left| -10 \right|cm$
$f=15cm$
$\begin{align}
  & \dfrac{1}{v}-\dfrac{1}{10}=\dfrac{1}{15} \\
 & \dfrac{1}{v}=\dfrac{1}{10}+\dfrac{1}{15}=\dfrac{3+2}{30}=\dfrac{5}{30}=\dfrac{1}{6} \\
 & v=6cm \\
\end{align}$
The image of the object will be formed at a distance of$6cm$beyond the convex mirror. It means virtual image.
Now,
Magnification of mirror is given as,
$m=\dfrac{-v}{u}$
Here, values should be put along with the sign
Putting values,
$\begin{align}
  & m=\dfrac{-6}{-10}=\dfrac{6}{10} \\
 & m=0.6<1 \\
\end{align}$
It means erect and diminished image.
The image of the object will be formed at a distance of $6cm$beyond the mirror. The nature of image will be virtual, erect and diminished.

Note:
For a convex mirror, the image formed is always virtual and erect. Virtual image means the image is formed beyond the mirror and we cannot obtain it on a screen as a real image.
While applying the Mirror formula, it should be kept in mind that we have to put only the magnitude of object distance. As the object distance is always negative, we have already considered it in the formula.
While calculating magnification, magnitude of object and image distance along with the sign conventions have to be considered.